Contents

Geometric Algebra in 2D

Geometric Algebra in 3D

Geometric Algebra in 2D

$$\begin{eqnarray} \left| { { \vec{e} }_{ i}} \right| &=& 1 \\ { \vec{e} }_{ i} { \vec{e} }_{ j} &=& { \delta }_{ is}\end{eqnarray}$$
All other vectors in the space $ { R }^{ 2}$ are linear combinations of the basis $ \left\{ { \vec{e} }_{ x} , { \vec{e} }_{ y}\right\}$.

$$\begin{eqnarray} \vec{u} &=& a { \vec{e} }_{ x} + b { \vec{e} }_{ y} \\ \vec{v} &=& c { \vec{e} }_{ x} + d { \vec{e} }_{ y}\end{eqnarray}$$Dot Product

$$ \vec{u} \cdot \vec{v}$$

Wedge Product

$$\begin{eqnarray} \vec{u} \wedge \vec{u} &=& 0 \\ \vec{u} \wedge \vec{v} &=& - \vec{v} \wedge \vec{u} \qquad \mbox{Anticummutativity}\end{eqnarray}$$It is distributive.

$$\begin{eqnarray} \vec{u} \wedge \vec{u} &=& \left( { a { \vec{e} }_{ x} + b { \vec{e} }_{ y}} \right) \wedge \left( { c { \vec{e} }_{ x} + d { \vec{e} }_{ y}} \right) \\ \vec{u} \wedge \vec{u} &=& \left( { a { \vec{e} }_{ x}} \right) \wedge \left( { c { \vec{e} }_{ x}} \right) + \left( { a { \vec{e} }_{ x}} \right) \wedge \left( { d { \vec{e} }_{ y}} \right) + \left( { b { \vec{e} }_{ y}} \right) \wedge \left( { c { \vec{e} }_{ x}} \right) + \left( { b { \vec{e} }_{ y}} \right) \wedge \left( { d { \vec{e} }_{ y}} \right) \\ \vec{u} \wedge \vec{u} &=& \left( { a { \vec{e} }_{ x}} \right) \wedge \left( { d { \vec{e} }_{ y}} \right) + \left( { b { \vec{e} }_{ y}} \right) \wedge \left( { c { \vec{e} }_{ x}} \right) \\ \vec{u} \wedge \vec{u} &=& \left( { a d { \vec{e} }_{ x}} \right) \wedge { \vec{e} }_{ y} - \left( { b c { \vec{e} }_{ x}} \right) \wedge { \vec{e} }_{ y} \\ \vec{u} \wedge \vec{u} &=& \left( { \left( { a d - b c} \right) { \vec{e} }_{ x}} \right) \wedge { \vec{e} }_{ y}\end{eqnarray}$$
Since we have

$$ { \vec{e} }_{ x} { \vec{e} }_{ y} = { \vec{e} }_{ x} \cdot { \vec{e} }_{ y} + { \vec{e} }_{ x} \wedge { \vec{e} }_{ y}$$

and the scalar product of orthogonal vectors is zero we finally get.

$$ \vec{u} \wedge \vec{u} = \left( { a d - b c} \right) { \vec{e} }_{ x} { \vec{e} }_{ y}$$

This equation allows us to calculate the magnitude of a bivector in 2D. From the defintion of the geometric product

$$\fbox{$ \displaystyle \vec{u} \vec{v} = \vec{u} \cdot \vec{v} + \vec{u} \wedge \vec{v} $} \qquad \mbox{Geomertic Product}$$
we immediately get

$$ \vec{u} \vec{u} = \left| { { \vec{u} }^{ 2}} \right|$$

and for orthogonal vetcor $ \vec{w}$ and $ \vec{f}$ we get

$$ \vec{w} \vec{f} = \vec{w} \wedge \vec{f} \qquad \mbox{for orthogonal vectors}$$

We put two 1-dimensional object sinto the geometric product and get the sum of a 0-dimensional object (a scalar) and a 2-dimension object (a bivector).

We do some magic with basis vectors.

$$ { \vec{e} }_{ 1} { \vec{e} }_{ 1} = { \vec{e} }_{ 1} \cdot { \vec{e} }_{ 1} + { \vec{e} }_{ 1} \wedge { \vec{e} }_{ 1} = { \vec{e} }_{ 1} \cdot { \vec{e} }_{ 1} = 1$$

$$ { \vec{e} }_{ 1} { \vec{e} }_{ 2} = { \vec{e} }_{ 1} \cdot { \vec{e} }_{ 2} + { \vec{e} }_{ 1} \wedge { \vec{e} }_{ 2} = { \vec{e} }_{ 1} \wedge { \vec{e} }_{ 2} = - { \vec{e} }_{ 2} \wedge { \vec{e} }_{ 1} = - { \vec{e} }_{ 2} { \vec{e} }_{ 1}$$

$$ {\left( { \vec{e} }_{ 1} { \vec{e} }_{ 2} \right)}^{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} = - { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 2} { \vec{e} }_{ 1} = - 1$$

$$ {\left( { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \right)}^{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} = { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 3} = - 1$$

$$ {\left( { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} \right)}^{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} = 1$$

We call the geometric product of basis vectors a pseudo-scalar. Attention, in 2D and 3D it turns out to be -1 but in 4D it is +1.

The set $ \left\{ 1 , { \vec{e} }_{ 1} , { \vec{e} }_{ 2} , { \vec{e} }_{ 1} { \vec{e} }_{ 2}\right\}$ forms the basis for $ G { R }^{ 2}$. The basis is four-dimensional. Any object in this object space can be written as a linear combination of these four basis vectors. These objects are called multi-vectors.

Rotations

$$\begin{eqnarray} z &=& { e }^{ i \varphi } \left( { a + b i} \right) \\ z &=& \left( { \cos { \varphi } + i \sin { \varphi } } \right) \left( { a + b i} \right) \\ z &=& \cos { \varphi } \left( { a + b i} \right) + i \sin { \varphi } \left( { a + b i} \right) \\ z &=& \cos { \varphi } a + \cos { \varphi } b i + i \sin { \varphi } a + i \sin { \varphi } b i \\ z &=& \cos { \varphi } a - \sin { \varphi } b + \cos { \varphi } b i + i \sin { \varphi } a \\ z &=& \cos { \varphi } a - \sin { \varphi } b + \left( { \cos { \varphi } b + \sin { \varphi } a} \right) i\end{eqnarray}$$
What happens if we multiply a vector $ \vec{u} = a { \vec{e} }_{ 1} + b { \vec{e} }_{ 2} $with $ I = { \vec{e} }_{ 1} { \vec{e} }_{ 2}$ in the right?

$$\begin{eqnarray} u I &=& \left( { a { \vec{e} }_{ 1} + b { \vec{e} }_{ 2}} \right) { \vec{e} }_{ 1} { \vec{e} }_{ 2} \\ u I &=& a { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} \\ u I &=& a { \vec{e} }_{ 2} - b { \vec{e} }_{ 1}\end{eqnarray}$$
Let's compare this to the result of the complex number rotation if we set $ \varphi = 90 \,^{\circ}$.

$$\begin{eqnarray} z &=& \cos { \varphi } a - \sin { \varphi } b + \left( { \cos { \varphi } b + \sin { \varphi } a} \right) i \\ z &=& - b + a i \\ z &=& - b + a i\end{eqnarray}$$
We got the same answer. Multiplying $ \vec{u} = a { \vec{e} }_{ 1} + b { \vec{e} }_{ 2}$ by $ I$ on the right obviously rotates rotates the vector $ \vec{u}$ by 90° CCW. How do we rotate by a different angle? Let's try the following

$$\begin{eqnarray} \vec{u'} &=& \vec{u} { e }^{ \varphi I} \\ \vec{u'} &=& \vec{u} \left( { \cos { \varphi } + \sin { \varphi } I} \right) \\ \vec{u'} &=& a { \vec{e} }_{ 1} \left( { \cos { \varphi } + \sin { \varphi } { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) + b { \vec{e} }_{ 2} \left( { \cos { \varphi } + \sin { \varphi } { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \\ \vec{u'} &=& a \cos { \varphi } { \vec{e} }_{ 1} + a \sin { \varphi } { \vec{e} }_{ 2} + b \cos { \varphi } { \vec{e} }_{ 2} + b \sin { \varphi } { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} \\ \vec{u'} &=& \left( { a \cos { \varphi } - b \sin { \varphi } } \right) { \vec{e} }_{ 1} + \left( { b \cos { \varphi } + a \sin { \varphi } } \right) { \vec{e} }_{ 2}\end{eqnarray}$$
That's the same expression we got for the complex number rotation. Let's multiply on the other side now.

$$\begin{eqnarray} \vec{v'} &=& { e }^{ \varphi I} \vec{v} \\ \vec{v'} &=& \left( { \cos { \varphi } + \sin { \varphi } I} \right) \vec{v} \\ \vec{v'} &=& \left( { \cos { \varphi } + \sin { \varphi } { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \left( { a { \vec{e} }_{ 1} + b { \vec{e} }_{ 2} } \right) \\ \vec{v'} &=& a \cos { \varphi } { \vec{e} }_{ 1} + b \cos { \varphi } { \vec{e} }_{ 2} + a \sin { \varphi } { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} + b \sin { \varphi } { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 2} \\ \vec{v'} &=& a \cos { \varphi } { \vec{e} }_{ 1} + b \cos { \varphi } { \vec{e} }_{ 2} - a \sin { \varphi } { \vec{e} }_{ 2} + b \sin { \varphi } { \vec{e} }_{ 1} \\ \vec{v'} &=& \left( { a \cos { \varphi } + b \sin { \varphi } } \right) { \vec{e} }_{ 1} + \left( { b \cos { \varphi } - a \sin { \varphi } } \right) { \vec{e} }_{ 2} \end{eqnarray}$$
Comparing both results yields in 2D with $ I = { \vec{e} }_{ 1} { \vec{e} }_{ 2}$

$$\fbox{$ \displaystyle \vec{u} { e }^{ \varphi I} = { e }^{ - \varphi I} \vec{u} $}$$

Multiplying with $ { e }^{ \theta I}$ on the right rotates CCW.

$$\fbox{$ \displaystyle \vec{u'} = \vec{u} { e }^{ \varphi I} $} \qquad \mbox{Rotating CCW}$$

Multiplying on the left rotates CW. For $ \varphi = 90 \,^{\circ}$ we have with $ { e }^{ \varphi I} = \cos { \varphi } + \sin { \varphi } I$

$$\begin{eqnarray} \vec{u} { e }^{ \varphi I} &=& { e }^{ - \varphi I} \vec{u} \\ \vec{u} \left( { \cos { \varphi } + \sin { \varphi } I} \right) &=& \left( { \cos { \varphi } - \sin { \varphi } I} \right) \vec{u} \\ \vec{u} I &=& - I \vec{u}\end{eqnarray}$$

Projections and Reflections

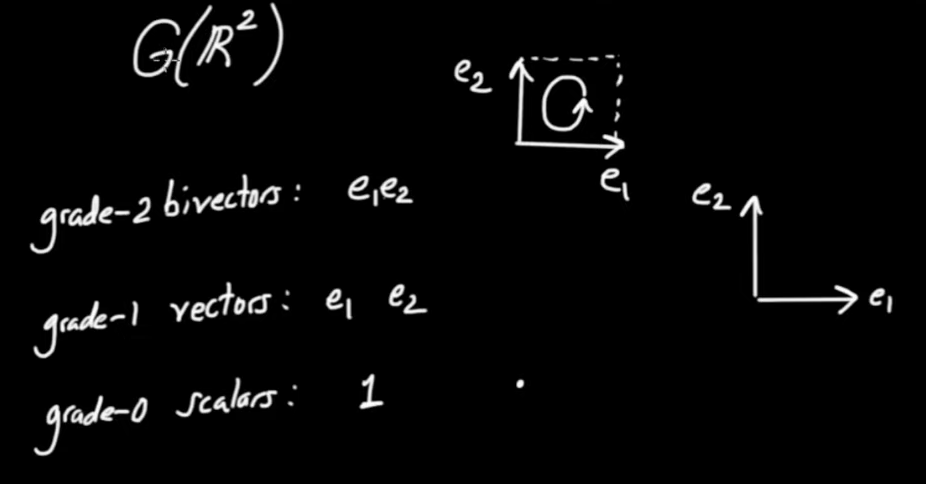One interesting point to note is

$$ \vec{u} \vec{u} = \vec{u} \cdot \vec{u} + \vec{u} \wedge \vec{u}$$

$$ \vec{u} \vec{u} = \vec{u} \cdot \vec{u} = { \left| { \vec{u}} \right| }^{ 2}$$
We can write this like so

$$ \frac{ \vec{u}}{ { \left| { \vec{u}} \right| }^{ 2}} \vec{u} = 1$$

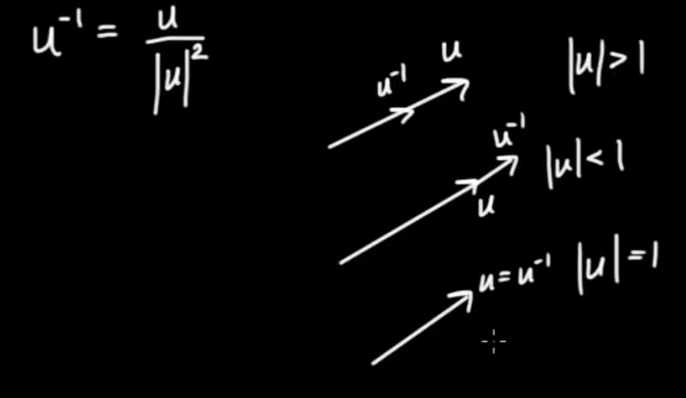
which means that we have identified the inverse of $ \vec{u}$

$$ { \vec{u} }^{ - 1} = \frac{ \vec{u}}{ { \left| { \vec{u}} \right| }^{ 2}}$$
or in other words a recipe for dividing by a vector $ \vec{u}$.

$$\fbox{$ \displaystyle \frac{ \vec{v}}{ { \left[ \vec{u}\right] }^{ right}} = \vec{v} \frac{ \vec{u}}{ { \left| { \vec{u}} \right| }^{ 2}} $} \qquad \mbox{Division by a vector on the right}$$

We use the construct
$$ \frac{ 1}{ { \left[ ...\right] }^{ right}}$$

to indicate that we divide on the right side. Dividing on the left side would be written like so

$$\fbox{$ \displaystyle \frac{ \vec{v}}{ { \left[ \vec{u}\right] }^{ left}} = \frac{ \vec{u}}{ { \left| { \vec{u}} \right| }^{ 2}} \vec{v} $} \qquad \mbox{Division by a vector on the left}$$

Here is a geometric interpretation of the inverse of a vector. It's a vector in the same direction but with different length.

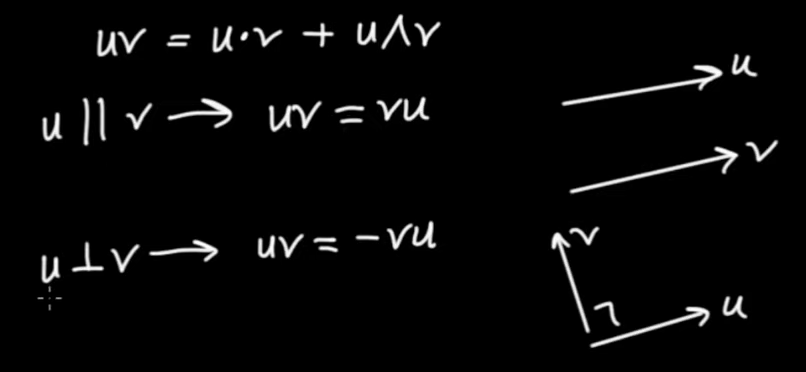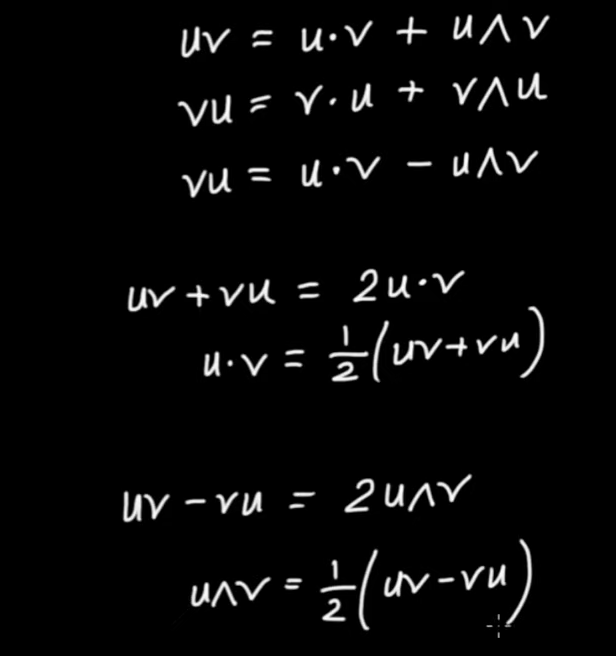$$ \vec{u} \cdot \vec{v} = \frac{ 1}{ 2} \left( { \vec{u} \vec{v} + \vec{v} \vec{u}} \right)$$

$$ \vec{u} \wedge \vec{v} = \frac{ 1}{ 2} \left( { \vec{u} \vec{v} - \vec{v} \vec{u}} \right)$$

Projection and Rejection

Let's see. We have vectors $ \vec{u}$ and $ \vec{v}$ and $ \vec{u}$ is a linear combination of the some component parallel to $ \vec{v}$ and another component perpendicular to $ \vec{v}$.

$$ \vec{u} = { \vec{u} }_{ par} + { \vec{u} }_{ perp}$$

We multiply that by $ \vec{v}$ and get

$$ \vec{u} \vec{v} = { \vec{u} }_{ par} \vec{v} + { \vec{u} }_{ perp} \vec{v}$$
Since $ { \vec{u} }_{ perp}$ is by definition perpendicular to $ \vec{v}$ we have

$$ { \vec{u} }_{ perp} \vec{v} = { \vec{u} }_{ perp} \wedge \vec{v} = - \vec{v} \wedge { \vec{u} }_{ perp} = - \vec{v} { u }_{ perp}$$

and therefore

$$\begin{eqnarray} \vec{u} \vec{v} &=& { \vec{u} }_{ par} \vec{v} - \vec{v} { \vec{u} }_{ perp} \\ \vec{u} \vec{v} &=& { \vec{u} }_{ par} \vec{v} - \vec{v} \left( { \vec{u} - { \vec{u} }_{ par}} \right) \\ \vec{u} \vec{v} &=& { \vec{u} }_{ par} \vec{v} - \vec{v} \vec{u} + \vec{v} { \vec{u} }_{ par} \\ \vec{u} \vec{v} &=& { \vec{u} }_{ par} \vec{v} - \vec{v} \vec{u} + { \vec{u} }_{ par} \vec{v} \\ \vec{u} \vec{v} + \vec{v} \vec{u} &=& 2 { \vec{u} }_{ par} \vec{v}\end{eqnarray}$$
$$ { \vec{u} }_{ par} \vec{v} = \frac{ 1}{ 2} \left( { \vec{u} \vec{v} + \vec{v} \vec{u}} \right) = \vec{u} \cdot \vec{v}$$

Nothing special about that. We multiply by $ { \vec{v} }^{ - 1}$

$$ { \vec{u} }_{ par} \vec{v} { \vec{v} }^{ - 1} = \left( { \vec{u} \cdot \vec{v}} \right) { \vec{v} }^{ - 1}$$

and get

$$\fbox{$ \displaystyle { \vec{u} }_{ par} = \left( { \vec{u} \cdot \vec{v}} \right) { \vec{v} }^{ - 1} $} \qquad \mbox{Projection}$$

We also want to determine an expression of $ { \vec{u} }_{ perp}$. Letz's see

$$\begin{eqnarray} { \vec{u} }_{ perp} &=& \vec{u} - { \vec{u} }_{ par} \\ { \vec{u} }_{ perp} &=& \vec{u} - \left( { \vec{u} \cdot \vec{v}} \right) { \vec{v} }^{ - 1} \\ { \vec{u} }_{ perp} &=& \left( { \vec{u} \vec{v} - \vec{u} \cdot \vec{v}} \right) { \vec{v} }^{ - 1}\end{eqnarray}$$
$$\fbox{$ \displaystyle { \vec{u} }_{ perp} = \left( { \vec{u} \wedge \vec{v}} \right) { \vec{v} }^{ - 1} $} \qquad \mbox{Rejection}$$

Let's remember that $ \vec{u} \wedge \vec{v}$ is actually equal to $ \vec{u} \vec{v}$ if both vectors are orthogonal and that multiplying with a bivector on the left rotatates a vector CW by the angle between the two vectors, in this case 90°. $ { \vec{v} }^{ - 1}$ is actually parallel to $ \vec{v}$ (just a scaled version). So multiplying this by 90 ° of course generates a vector that is perpendicular to $ \vec{v}$.

Let's try this. Given are

$$\begin{eqnarray} \vec{u} &=& { \vec{e} }_{ 1} + { \vec{e} }_{ 2} \\ \vec{v} &=& 2 { \vec{e} }_{ 1}\end{eqnarray}$$
We are looking for the projection of $ \vec{u}$ on to $ \vec{v}$ ($ { \vec{u} }_{ par}$ being parallel to $ \vec{v}$) and also the rejection ($ { \vec{u} }_{ perp}$ being perpendicular to $ \vec{v}$). We have

$$\begin{eqnarray} { \vec{u} }_{ par} &=& \left( { \vec{u} \cdot \vec{v}} \right) { \vec{v} }^{ - 1} \\ { \vec{u} }_{ par} &=& \left( { \vec{u} \cdot \vec{v}} \right) \frac{ \vec{v}}{ { \left| { \vec{v}} \right| }^{ 2}} \\ { \vec{u} }_{ par} &=& 2 \frac{ 2 { \vec{e} }_{ 1}}{ { \left| { 2 { \vec{e} }_{ 1}} \right| }^{ 2}}\end{eqnarray}$$
$$ { \vec{u} }_{ par} = 2 \frac{ 1}{ 2} { \vec{e} }_{ 1} = { \vec{e} }_{ 1}$$
And we have

$$\begin{eqnarray} { \vec{u} }_{ perp} &=& \left( { \vec{u} \wedge \vec{v}} \right) { \vec{v} }^{ - 1} \\ { \vec{u} }_{ perp} &=& \left( { \vec{u} \wedge \vec{v}} \right) \frac{ \vec{v}}{ { \left| { \vec{v}} \right| }^{ 2}} \\ { \vec{u} }_{ perp} &=& \left( { \vec{u} \wedge \vec{v}} \right) \frac{ 1}{ 2} { \vec{e} }_{ 1} \\ { \vec{u} }_{ perp} &=& \left( { \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) \wedge \left( { 2 { \vec{e} }_{ 1}} \right)} \right) \frac{ 1}{ 2} { \vec{e} }_{ 1} \\ { \vec{u} }_{ perp} &=& \left( { { \vec{e} }_{ 1} \wedge \left( { 2 { \vec{e} }_{ 1}} \right) + { \vec{e} }_{ 2} \wedge \left( { 2 { \vec{e} }_{ 1}} \right)} \right) \frac{ 1}{ 2} { \vec{e} }_{ 1} \\ { \vec{u} }_{ perp} &=& \left( { { \vec{e} }_{ 2} \wedge \left( { 2 { \vec{e} }_{ 1}} \right)} \right) \frac{ 1}{ 2} { \vec{e} }_{ 1} \\ { \vec{u} }_{ perp} &=& \left( { { \vec{e} }_{ 2} \wedge { \vec{e} }_{ 1}} \right) { \vec{e} }_{ 1} \\ { \vec{u} }_{ perp} &=& { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 1}\end{eqnarray}$$
$$ { \vec{u} }_{ perp} = { \vec{e} }_{ 2}$$

Reflection

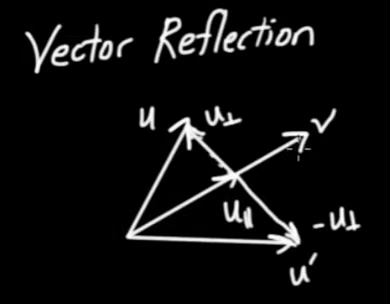$$\begin{eqnarray} \vec{u'} &=& { \vec{u} }_{ par} - { \vec{u} }_{ perp} \\ \vec{v} \vec{u'} &=& \vec{v} { \vec{u} }_{ par} - \vec{v} { \vec{u} }_{ perp} \\ \vec{v} \vec{u'} &=& { \vec{u} }_{ par} \vec{v} + { \vec{u} }_{ perp} \vec{v} \\ \vec{v} \vec{u'} &=& \left( { { \vec{u} }_{ par} + { \vec{u} }_{ perp}} \right) \vec{v} \\ \vec{v} \vec{u'} &=& \vec{u} \vec{v} \\ { \vec{v} }^{ - 1} \vec{v} \vec{u'} &=& { \vec{v} }^{ - 1} \vec{u} \vec{v}\end{eqnarray}$$
$$\fbox{$ \displaystyle \vec{u'} = { \vec{v} }^{ - 1} \vec{u} \vec{v} $} \qquad \mbox{Reflection}$$

$$ \vec{u'} = { \vec{v} }^{ - 1} \vec{u} \vec{v}$$

Example:

$$\begin{eqnarray} \vec{u} &=& { \vec{e} }_{ 1} + { \vec{e} }_{ 2} \\ \vec{v} &=& { \vec{e} }_{ 1}\end{eqnarray}$$

$$\begin{eqnarray} \vec{u'} &=& { \vec{v} }^{ - 1} \vec{u} \vec{v} \\ \vec{u'} &=& { \vec{e} }_{ 1} \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) { \vec{e} }_{ 1} \\ \vec{u'} &=& { \vec{e} }_{ 1} \left( { { \vec{e} }_{ 1} { \vec{e} }_{ 1} + { \vec{e} }_{ 2} { \vec{e} }_{ 1}} \right) \\ \vec{u'} &=& { \vec{e} }_{ 1} + { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} \\ \vec{u'} &=& { \vec{e} }_{ 1} - { \vec{e} }_{ 2}\end{eqnarray}$$

Rotation by reflecting twice

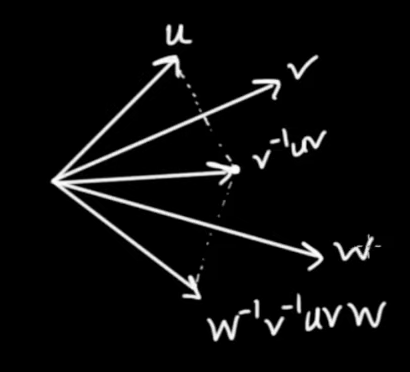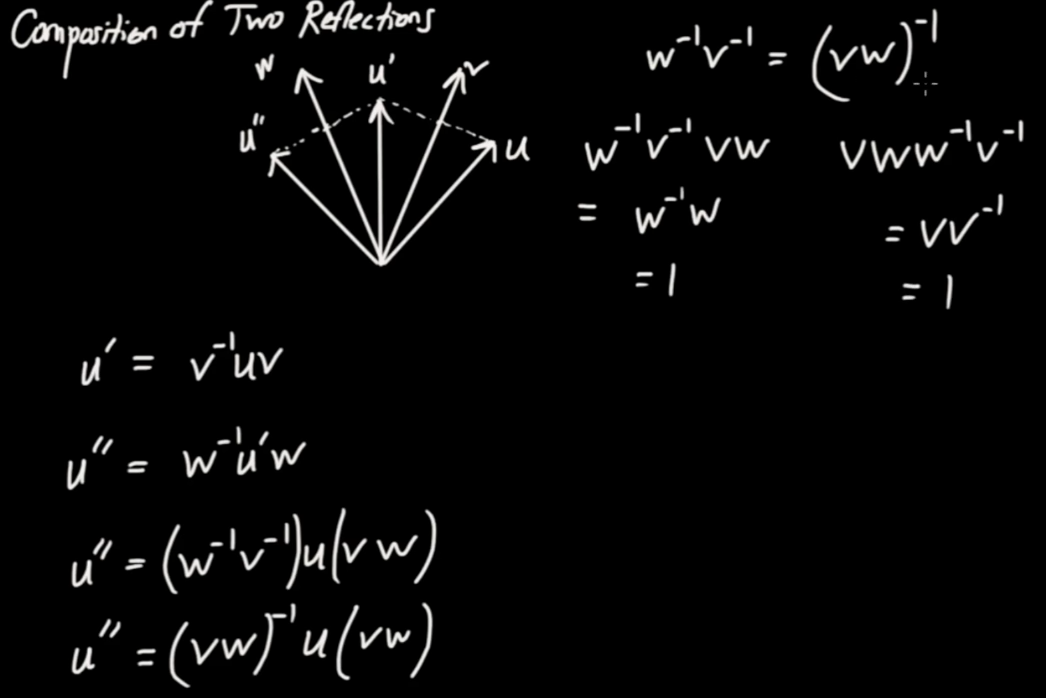
The first reflection of $ \vec{u}$ is

$$ { \vec{v} }^{ - 1} \vec{u} \vec{v}$$

After reflecting across $ \vec{w}$ we get

$$ { \vec{w} }^{ - 1} { \vec{v} }^{ - 1} \vec{u} \vec{v} \vec{w}$$

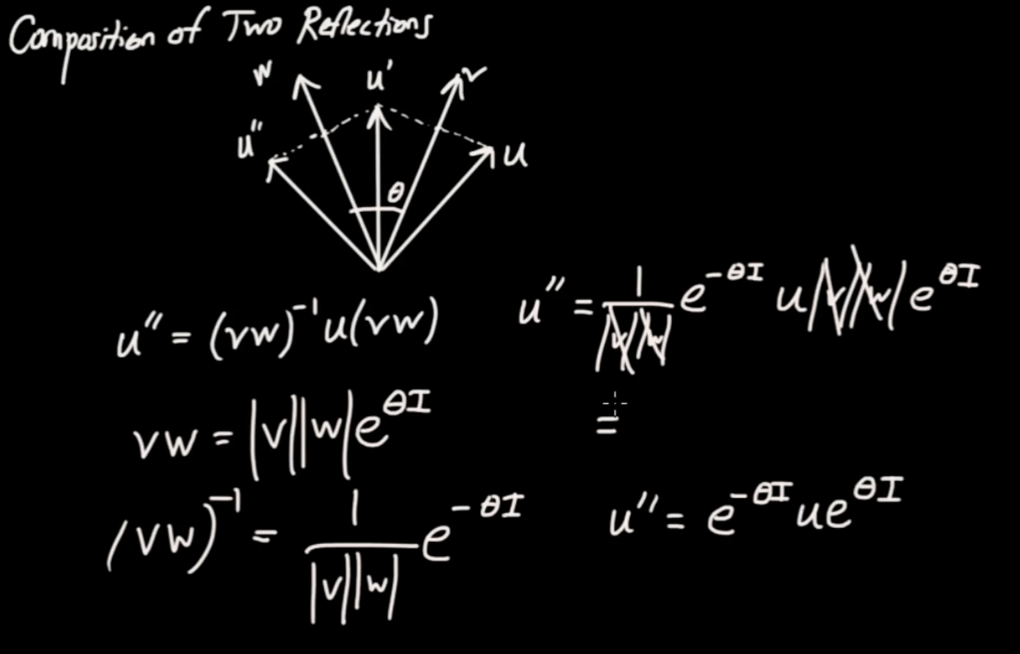
Considering the above figure we can see that reflecting first across $ \vec{v}$ and then across $ \vec{w}$ is identical to rotating by an angle twice as big as the angle between $ \vec{w}$ and $ \vec{v}$. Let be $ \varphi = 2 \theta $ and $ \theta $ be the angle from $ \vec{v}$ to $ \vec{w}$ . We then get the rotation of $ \vec{u}$ by an angle $ \varphi $ like so.

$$\fbox{$ \displaystyle \vec{u'} = { \vec{w} }^{ - 1} { \vec{v} }^{ - 1} \vec{u} \vec{v} \vec{w} $} \qquad \mbox{Rotation by twice the angle from v to w}$$

Trigonometry

We have also found the following:

We have a deeper look on the last equation given here.

$$\begin{eqnarray} \vec{u} \vec{v} &=& \left| { \vec{u}} \right| \left| { \vec{v}} \right| { e }^{ \theta I} \\ \vec{u} \vec{v} &=& \left| { \vec{u}} \right| \left| { \vec{v}} \right| \left( { \cos { \theta } + \sin { \theta } { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \\ \vec{u} \vec{v} &=& \left| { \vec{u}} \right| \left| { \vec{v}} \right| \cos { \theta } + \left| { \vec{u}} \right| \left| { \vec{v}} \right| \sin { \theta } { \vec{e} }_{ 1} { \vec{e} }_{ 2} \\ \vec{u} \vec{v} &=& \vec{u} \cdot \vec{v} + \vec{u} \wedge \vec{v}\end{eqnarray}$$

Law of sines

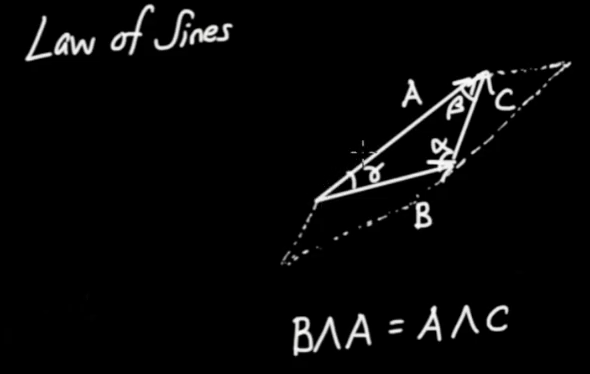Let's see. We have

$$ \vec{A} = \vec{B} + \vec{C}$$

and therefore

$$ \vec{B} = \vec{A} - \vec{C}$$

and then

$$ \vec{B} \wedge \vec{A} = \left( { \vec{A} - \vec{C}} \right) \wedge \vec{A} = \vec{A} \wedge \vec{A} - \vec{C} \wedge \vec{A} = - \vec{C} \wedge \vec{A}$$

$$ \vec{B} \wedge \vec{A} = \vec{A} \wedge \vec{C}$$

We now replace the wedge products with the formuals given above.

$$ \left| { \vec{B}} \right| \left| { \vec{A}} \right| \sin { \gamma } I = \left| { \vec{A}} \right| \left| { \vec{C}} \right| \sin { \beta } I$$

$$\begin{eqnarray} B A \sin { \gamma } &=& A C \sin { \beta } \\ B \sin { \gamma } &=& C \sin { \beta } \end{eqnarray}$$
$$\fbox{$ \displaystyle \frac{ \sin { \gamma } }{ C} = \frac{ \sin { \beta } }{ B} $} \qquad \mbox{Law of sines}$$

Law of cosines

$$ \vec{A} = \vec{B} + \vec{C}$$

$$ \vec{C} = \vec{A} - \vec{B}$$

$$\begin{eqnarray} { \vec{C} }^{ 2} &=& \left( { \vec{A} - \vec{B}} \right) \left( { \vec{A} - \vec{B}} \right) \\ { \vec{C} }^{ 2} &=& { \vec{A} }^{ 2} - \vec{A} \vec{B} - \vec{B} \vec{A} + { \vec{B} }^{ 2} \\ { \vec{C} }^{ 2} &=& { A }^{ 2} + { B }^{ 2} - \left( { \vec{A} \vec{B} + \vec{B} \vec{A}} \right) \\ { \vec{C} }^{ 2} &=& { A }^{ 2} + { B }^{ 2} - \left( { 2 \vec{A}} \right) \cdot \vec{B}\end{eqnarray}$$
$$\fbox{$ \displaystyle { C }^{ 2} = { A }^{ 2} + { B }^{ 2} - 2 A B \cos { \gamma } $} \qquad \mbox{Law of cosines}$$

Linear Algebra and Cramer's Rule

$$\begin{eqnarray} \vec{u} \wedge \vec{u} &=& \left( { a { \vec{e} }_{ x} + b { \vec{e} }_{ y}} \right) \wedge \left( { c { \vec{e} }_{ x} + d { \vec{e} }_{ y}} \right) \\ \vec{u} \wedge \vec{u} &=& \left( { a { \vec{e} }_{ x}} \right) \wedge \left( { c { \vec{e} }_{ x}} \right) + \left( { a { \vec{e} }_{ x}} \right) \wedge \left( { d { \vec{e} }_{ y}} \right) + \left( { b { \vec{e} }_{ y}} \right) \wedge \left( { c { \vec{e} }_{ x}} \right) + \left( { b { \vec{e} }_{ y}} \right) \wedge \left( { d { \vec{e} }_{ y}} \right) \\ \vec{u} \wedge \vec{u} &=& \left( { a { \vec{e} }_{ x}} \right) \wedge \left( { d { \vec{e} }_{ y}} \right) + \left( { b { \vec{e} }_{ y}} \right) \wedge \left( { c { \vec{e} }_{ x}} \right) \\ \vec{u} \wedge \vec{u} &=& \left( { a d { \vec{e} }_{ x}} \right) \wedge { \vec{e} }_{ y} - \left( { b c { \vec{e} }_{ x}} \right) \wedge { \vec{e} }_{ y} \\ \vec{u} \wedge \vec{u} &=& \left( { \left( { a d - b c} \right) { \vec{e} }_{ x}} \right) \wedge { \vec{e} }_{ y}\end{eqnarray}$$

Solving systems of linear equations

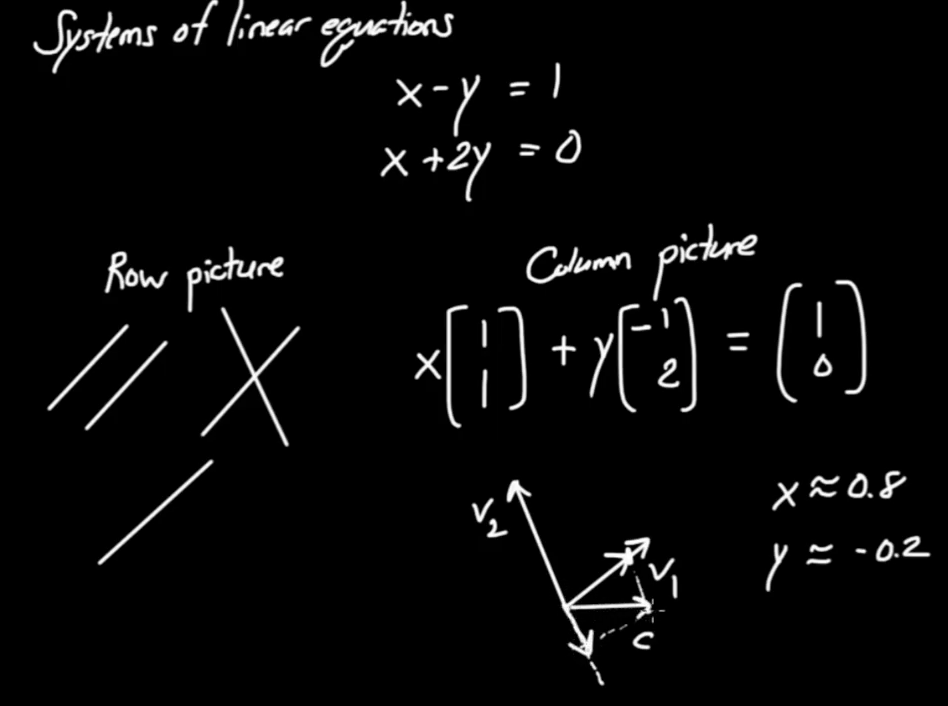$$ x = \frac{ \vec{c} \wedge \vec{b}}{ \vec{a} \wedge \vec{b}}$$ $$ y = \frac{ \vec{a} \wedge \vec{c}}{ \vec{a} \wedge \vec{b}}$$

Example:

$$\begin{eqnarray} x - y &=& 1 \\ x + 2 y &=& 0\end{eqnarray}$$
We therefore have

$$\begin{eqnarray} \vec{a} &=& \left( \begin{array}{c} 1\\ 1 \end{array}\right) &=& { \vec{e} }_{ 1} + { \vec{e} }_{ 2} \\ \vec{b} &=& \left( \begin{array}{c} - 1\\ 2 \end{array}\right) &=& - { \vec{e} }_{ 1} + 2 { \vec{e} }_{ 2} \\ \vec{c} &=& \left( \begin{array}{c} 1\\ 0 \end{array}\right) &=& { \vec{e} }_{ 1}\end{eqnarray}$$
Substituting this into

$$ x = \frac{ \vec{c} \wedge \vec{b}}{ \vec{a} \wedge \vec{b}}$$
gives

$$ x = \frac{ { \vec{e} }_{ 1} \wedge \left( { - { \vec{e} }_{ 1} + 2 { \vec{e} }_{ 2}} \right)}{ \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) \wedge \left( { - { \vec{e} }_{ 1} + 2 { \vec{e} }_{ 2}} \right)}$$

$$\begin{eqnarray} x &=& \frac{ - { \vec{e} }_{ 1} \wedge { \vec{e} }_{ 1} + { \vec{e} }_{ 1} \wedge \left( { 2 { \vec{e} }_{ 2}} \right)}{ - \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) \wedge { \vec{e} }_{ 1} + \left( { 2 \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right)} \right) \wedge { \vec{e} }_{ 2}} \\ x &=& \frac{ { \vec{e} }_{ 1} \wedge \left( { 2 { \vec{e} }_{ 2}} \right)}{ - { \vec{e} }_{ 2} \wedge { \vec{e} }_{ 1} + \left( { 2 { \vec{e} }_{ 1}} \right) \wedge { \vec{e} }_{ 2}} \\ x &=& \frac{ { \vec{e} }_{ 1} \wedge \left( { 2 { \vec{e} }_{ 2}} \right)}{ \left( { 3 { \vec{e} }_{ 1}} \right) \wedge { \vec{e} }_{ 2}} \\ x &=& \frac{ 2}{ 3}\end{eqnarray}$$

More on reflections

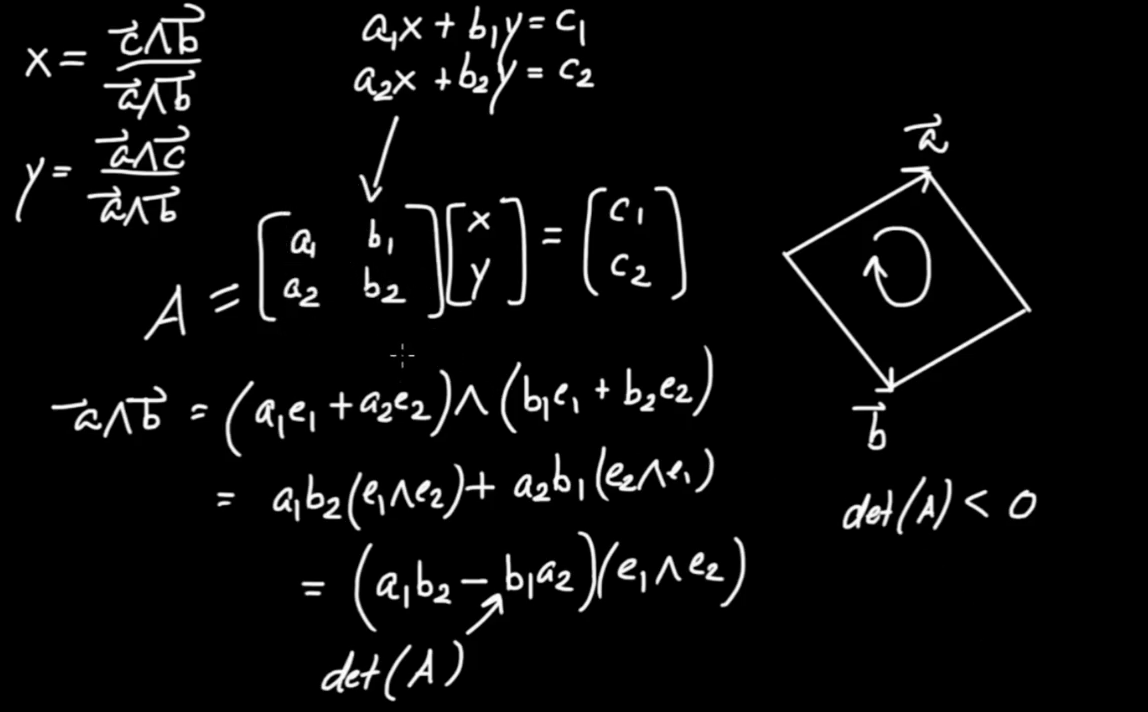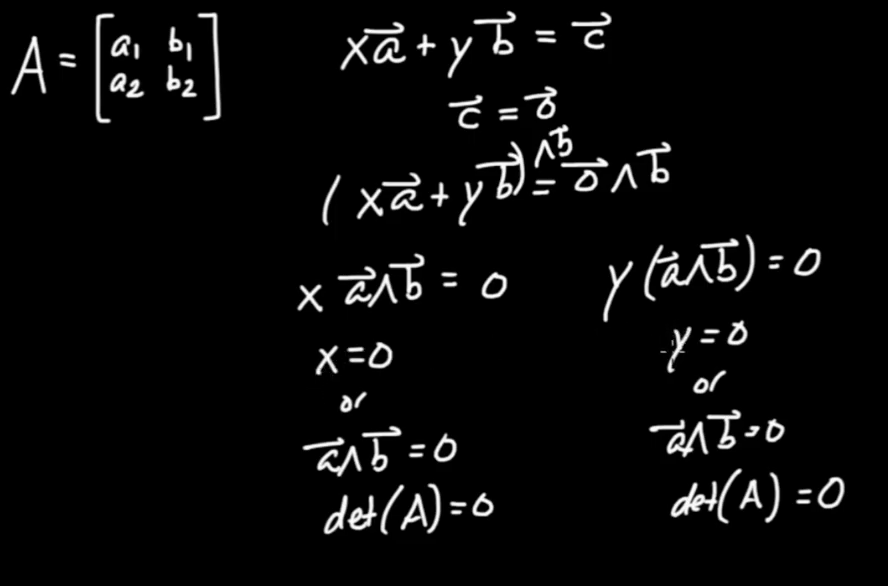In Rotations we have shown the following

$$ { e }^{ - \theta I} \vec{u} = \vec{u} { e }^{ \theta I} \qquad \mbox{In 2D only}$$

Note, that we used $ I = { \vec{e} }_{ 1} { \vec{e} }_{ 2}$ to prove that. So this equation is valid in 2D only. In Reflection we discussed reflections. In that derivation we made no dimension-based assumptions and got

$$\fbox{$ \displaystyle \vec{u'} = { \vec{v} }^{ - 1} \vec{u} \vec{v} $} \qquad \mbox{Reflection}$$
for relfecting $ \vec{u}$ across $ \vec{v}$ and

$$\fbox{$ \displaystyle \vec{u'} = { \vec{w} }^{ - 1} { \vec{v} }^{ - 1} \vec{u} \vec{v} \vec{w} $} \qquad \mbox{Rotation by the angle from v to w}$$

for a rotation by twice the angle from $ \vec{v}$ to $ \vec{w}$. This works in all dimensions under the assumption that all vectors share the same plane.

$$\begin{eqnarray} \vec{u} \vec{v} &=& \vec{u} \cdot \vec{v} + \vec{u} \wedge \vec{v} \\ \vec{u} \vec{v} &=& \left| { \vec{u}} \right| \left| { \vec{v}} \right| \cos { \varphi } + \left| { \vec{u}} \right| \left| { \vec{v}} \right| \sin { \varphi } I \\ \vec{u} \vec{v} &=& \left| { \vec{u}} \right| \left| { \vec{v}} \right| { e }^{ \varphi I}\end{eqnarray}$$

$$\begin{eqnarray} \vec{u'} &=& { \vec{u} }_{ par} - { \vec{u} }_{ perp} \\ \vec{v} \vec{u'} &=& \vec{v} { \vec{u} }_{ par} - \vec{v} { \vec{u} }_{ perp} \\ \vec{v} \vec{u'} &=& { \vec{u} }_{ par} \vec{v} + { \vec{u} }_{ perp} \vec{v} \\ \vec{v} \vec{u'} &=& \left( { { \vec{u} }_{ par} + { \vec{u} }_{ perp}} \right) \vec{v} \\ \vec{v} \vec{u'} &=& \vec{u} \vec{v}\end{eqnarray}$$
$$\fbox{$ \displaystyle \vec{u'} = { \vec{v} }^{ - 1} \vec{u} \vec{v} $}$$

For $ \left| { \vec{v}} \right| = 1$ we have $ { \vec{v} }^{ - 1} = \vec{v}$ and thus
$$ \vec{u'} = \vec{v} \vec{u} \vec{v}$$ simplified version for $ \left| { \vec{v}} \right| = 1$

Kepler Problem

$$\fbox{$ \displaystyle \ddot{\vec{r}} = - \frac{ \mu }{ { r }^{ 2}} { \vec{e} }_{ r} $} \tag{1}$$ with $$ \mu = \gamma \left( { { m }_{ 1} + { m }_{ 2}} \right)$$

We do a quick view on angular momentum

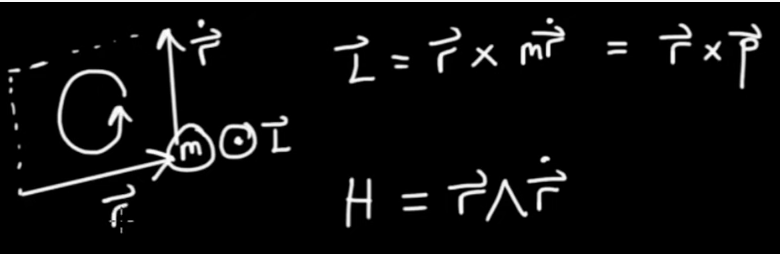$$\fbox{$ \displaystyle H = \vec{r} \wedge \dot{\vec{r}} $}$$

$$\begin{eqnarray} \frac{d { H} }{\, dt} &=& \dot{\vec{r}} \wedge \dot{\vec{r}} + \vec{r} \wedge \ddot{\vec{r}} \\ \frac{d { H} }{\, dt} &=& \vec{r} \wedge \ddot{\vec{r}}\end{eqnarray}$$
From Eq. 1 we know that $ \vec{r}$ and $ \ddot{\vec{r}}$ are parallel and so we have

$$ \frac{d { H} }{\, dt} = 0$$ $$ H = const$$

This means that the angular momentum is conserved.

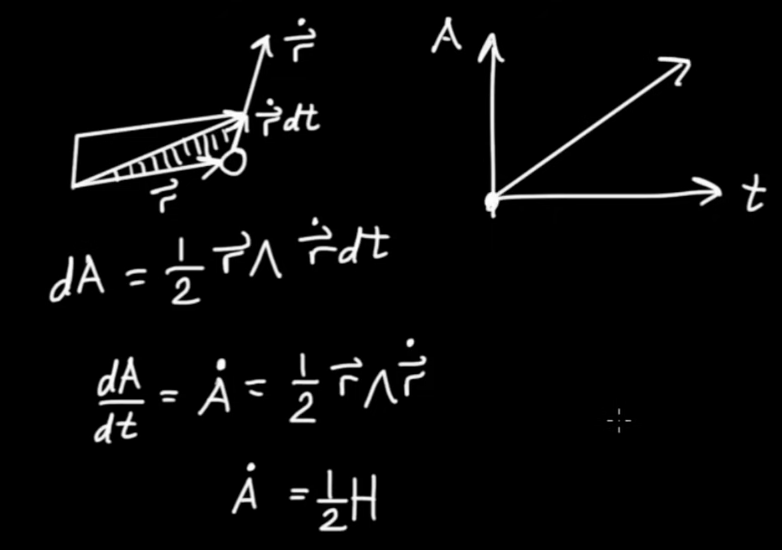$$ H = \vec{r} \wedge \dot{\vec{r}}$$

$$\begin{eqnarray} \vec{r} &=& r { \vec{e} }_{ r} \\ \dot{\vec{r}} &=& \dot{r} { \vec{e} }_{ r} + r { \dot{\vec{e}} }_{ r}\end{eqnarray}$$

$$\begin{eqnarray} H &=& \left( { r { \vec{e} }_{ r}} \right) \wedge \left( { \dot{r} { \vec{e} }_{ r} + r { \dot{\vec{e}} }_{ r}} \right) \\ H &=& \left( { r { \vec{e} }_{ r}} \right) \wedge \left( { \dot{r} { \vec{e} }_{ r}} \right) + \left( { r { \vec{e} }_{ r}} \right) \wedge \left( { r { \dot{\vec{e}} }_{ r}} \right) \\ H &=& \left( { r \dot{r} { \vec{e} }_{ r}} \right) \wedge { \vec{e} }_{ r} + \left( { { r }^{ 2} { \vec{e} }_{ r}} \right) \wedge { \dot{\vec{e}} }_{ r} \\ H &=& \left( { { r }^{ 2} { \vec{e} }_{ r}} \right) \wedge { \dot{\vec{e}} }_{ r} \\ H &=& { r }^{ 2} \left( { { \vec{e} }_{ r} { \dot{\vec{e}} }_{ r} - { \vec{e} }_{ r} \cdot { \dot{\vec{e}} }_{ r}} \right)\end{eqnarray}$$

$$ { \vec{e} }_{ r} \cdot { \dot{\vec{e}} }_{ r} = \frac{ 1}{ 2} \frac{d\left( { { \vec{e} }_{ r} \cdot { \vec{e} }_{ r}} \right)}{\, dt} = \frac{ 1}{ 2} \frac{d\left( { { \left| { { \vec{e} }_{ r}} \right| }^{ 2}} \right)}{\, dt} = 0 \tag{2}$$
We can therefore simplify to

$$\fbox{$ \displaystyle H = \vec{r} \wedge \dot{\vec{r}} = { r }^{ 2} { \vec{e} }_{ r} { \dot{\vec{e}} }_{ r} $} \qquad \mbox{Conserved angular momentum} \tag{3}$$

We have shown above that $ H$ is constant due to $ { \vec{e} }_{ r}$ and $ { \ddot{e} }_{ r}$ being parallel. We now have a concrete expression to quantify the angular momentum per unit mass. We revisit

$$ \ddot{\vec{r}} = - \frac{ \mu }{ { r }^{ 2}} { \vec{e} }_{ r}$$ with $$ \mu = \gamma \left( { { m }_{ 1} + { m }_{ 2}} \right)$$
and multiply this equation with $ \dot{\vec{r}}$.

$$\begin{eqnarray} \ddot{\vec{r}} \cdot \dot{\vec{r}} &=& - \left( { \frac{ \mu }{ { r }^{ 2}} { \vec{e} }_{ r}} \right) \cdot \dot{\vec{r}} \\ \frac{ 1}{ 2} \frac{d\left( { \dot{\vec{r}} \cdot \dot{\vec{r}}} \right)}{\, dt} &=& - \left( { \frac{ \mu }{ { r }^{ 2}} { \vec{e} }_{ r}} \right) \cdot \dot{\vec{r}}\end{eqnarray}$$
We have already seen above that by making use of the chain rule we get

$$ \dot{\vec{r}} = \dot{r} { \vec{e} }_{ r} + r { \dot{\vec{e}} }_{ r}$$

We therefore have

$$\begin{eqnarray} \frac{ 1}{ 2} \frac{d\left( { \dot{\vec{r}} \cdot \dot{\vec{r}}} \right)}{\, dt} &=& - \left( { \frac{ \mu }{ { r }^{ 2}} { \vec{e} }_{ r}} \right) \cdot \left( { \dot{r} { \vec{e} }_{ r} + r { \dot{\vec{e}} }_{ r}} \right) \\ \frac{ 1}{ 2} \frac{d\left( { { \left| { \dot{\vec{r}}} \right| }^{ 2}} \right)}{\, dt} &=& - \frac{ \mu }{ { r }^{ 2}} \left( { \left( { \dot{r} { \vec{e} }_{ r}} \right) \cdot { \vec{e} }_{ r} + \left( { r { \vec{e} }_{ r}} \right) \cdot { \dot{\vec{e}} }_{ r}} \right) \\ \frac{ 1}{ 2} \frac{d\left( { { v }^{ 2}} \right)}{\, dt} &=& - \frac{ \mu }{ { r }^{ 2}} \dot{r}\end{eqnarray}$$
$$\begin{eqnarray} \frac{ 1}{ 2} \frac{d\left( { { v }^{ 2}} \right)}{\, dt} &=& - \mu \frac{ \dot{r}}{ { r }^{ 2}} &=& \mu \frac{d\left( { { r }^{ - 1}} \right)}{\, dt} \\ \frac{ 1}{ 2} \frac{d\left( { { v }^{ 2}} \right)}{\, dt} - \mu \frac{d\left( { { r }^{ - 1}} \right)}{\, dt} &=& 0 \\ \frac{d\left( { \frac{ 1}{ 2} { v }^{ 2} - \mu \frac{ 1}{ r}} \right)}{\, dt} &=& 0\end{eqnarray}$$
We integrate this and need to come up with an integration constant. The integrand looks like energy per unit mass so let's take $ { E }_{ m}$

$$ \frac{ 1}{ 2} { v }^{ 2} - \mu \frac{ 1}{ r} = { E }_{ m}$$

We define

$$ T = \frac{ 1}{ 2} { v }^{ 2} \qquad \mbox{Kinetic Energy per unit mass}$$

$$ U = - \mu \frac{ 1}{ r} \qquad \mbox{Potential Energy per unit mass}$$

$$\fbox{$ \displaystyle { E }_{ m} = T + U = const $} \qquad \mbox{Conserved Total Energy per unit mass}$$

The kinetic and potential energy may change but the total energy of the orbiting mass is constant. Note, that we have a constant bivector $ H$ (angular momentum per unit mass) and a constant scalar $ { E }_{ m}$ (energy per unit mass). Let's now have a look on the law of gravitation (observation) and the expression for the angular momentum derived above

$$ H = { r }^{ 2} { \vec{e} }_{ r} { \dot{\vec{e}} }_{ r}$$ $$ \ddot{\vec{r}} = - \frac{ \mu }{ { r }^{ 2}} { \vec{e} }_{ r}$$
and multiply both equations.

$$\begin{eqnarray} H \ddot{\vec{r}} &=& - { r }^{ 2} { \vec{e} }_{ r} { \dot{\vec{e}} }_{ r} \frac{ \mu }{ { r }^{ 2}} { \vec{e} }_{ r} \\ H \ddot{\vec{r}} &=& - \mu { \vec{e} }_{ r} { \dot{\vec{e}} }_{ r} { \vec{e} }_{ r}\end{eqnarray}$$
We know from Eq. 2 that $ { \vec{e} }_{ r}$ and $ { \dot{\vec{e}} }_{ r}$ are orthogonal. This means we can flip the order if we flip the sign.

$$\begin{eqnarray} H \ddot{\vec{r}} &=& \mu { \dot{\vec{e}} }_{ r} { \vec{e} }_{ r} { \vec{e} }_{ r} \\ H \ddot{\vec{r}} &=& \mu { \dot{\vec{e}} }_{ r} \\ H \ddot{\vec{r}} - \mu { \dot{\vec{e}} }_{ r} &=& 0 \\ \frac{d\left( { H \dot{\vec{r}} - \mu { \vec{e} }_{ r}} \right)}{\, dt} &=& 0\end{eqnarray}$$We define $ \vec{c}$ to be a constant vector and call that the Laplace vector.

$$\fbox{$ \displaystyle H \dot{\vec{r}} - \mu { \vec{e} }_{ r} = \vec{c} $} \qquad \mbox{Conserved vector quantity}$$

$$ H \dot{\vec{r}} = \vec{c} + \mu { \vec{e} }_{ r}$$

We multiply the complete equation with $ \vec{r}$.
$$\begin{eqnarray} H \dot{\vec{r}} \vec{r} &=& \vec{c} \vec{r} + \mu { \vec{e} }_{ r} \vec{r} \\ H \left( { \dot{\vec{r}} \cdot \vec{r} + \dot{\vec{r}} \wedge \vec{r}} \right) &=& \vec{c} \cdot \vec{r} + \vec{c} \wedge \vec{r} + \left( { \mu { \vec{e} }_{ r}} \right) \cdot \vec{r} \\ H \left( { \dot{\vec{r}} \cdot \vec{r} - H} \right) &=& c r \cos { \theta } + \vec{c} \wedge \vec{r} + \mu r \\ H \left( { \dot{\vec{r}} \cdot \vec{r}} \right) - { H }^{ 2} &=& c r \cos { \theta } + \vec{c} \wedge \vec{r} + \mu r\end{eqnarray}$$
$$ H = h { \vec{e} }_{ x} { \vec{e} }_{ y}$$ $$ { H }^{ 2} = { h }^{ 2} {\left( { \vec{e} }_{ x} { \vec{e} }_{ y} \right)}^{ 2} = - { h }^{ 2}$$

$$ H \left( { \dot{\vec{r}} \cdot \vec{r}} \right) + { h }^{ 2} = c r \cos { \theta } + \vec{c} \wedge \vec{r} + \mu r$$

We have scalar, vector and bivector parts in this equation. we start with equating teh scalar part.

$$\begin{eqnarray} { h }^{ 2} &=& c r \cos { \theta } + \mu r \\ { h }^{ 2} &=& \left( { c \cos { \theta } + \mu } \right) r\end{eqnarray}$$
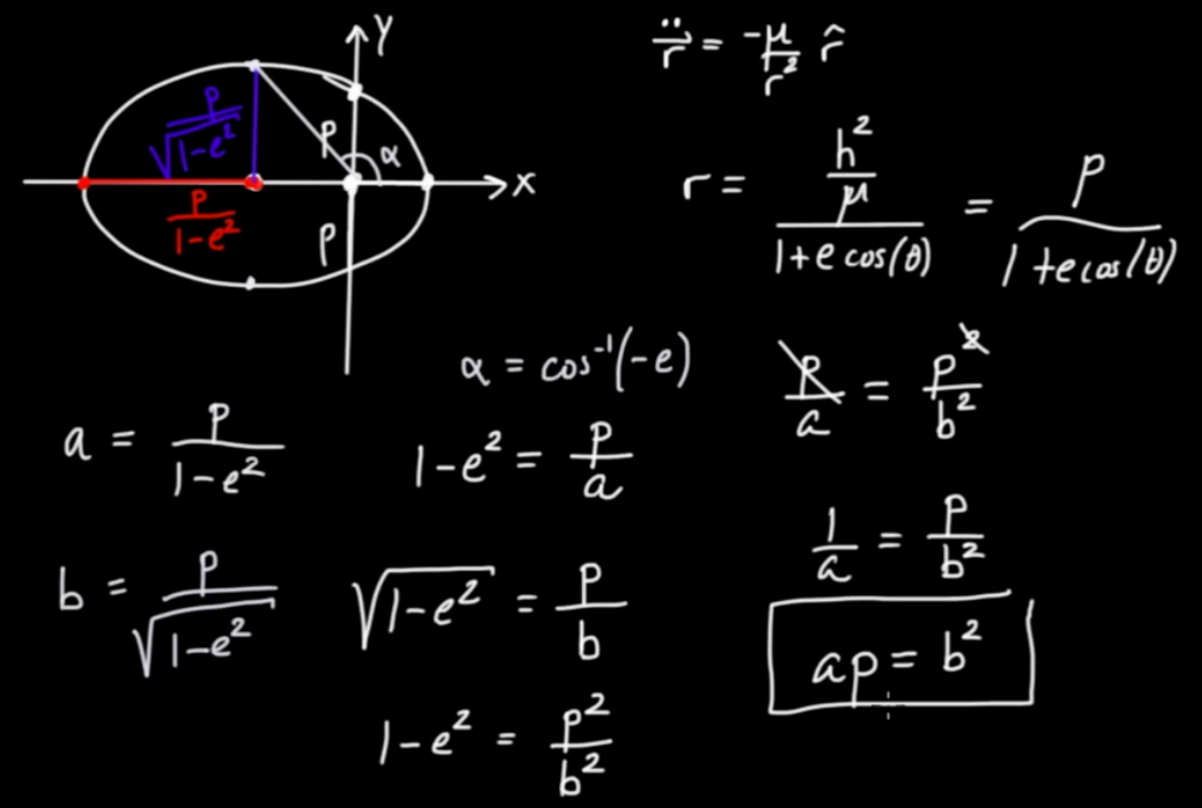
$$ r = \frac{ { h }^{ 2}}{ c \cos { \theta } + \mu }$$

$$ r = \frac{ \frac{ { h }^{ 2}}{ \mu }}{ 1 + \frac{ c}{ \mu } \cos { \theta } }$$

$$ p = \frac{ { h }^{ 2}}{ \mu } \qquad \mbox{semi latus rectum}$$

$$ e = \frac{ c}{ \mu } \qquad \mbox{eccentricity}$$

$$\fbox{$ \displaystyle r = \frac{ p}{ 1 + e \cos { \theta } } $}$$

$$\begin{eqnarray} r + e r \cos { \theta } &=& p \\ r + e x &=& p \\ r &=& p - e x \\ { r }^{ 2} &=& {\left( p - e x \right)}^{ 2} \\ { x }^{ 2} + { y }^{ 2} &=& { p }^{ 2} - 2 p e x + { e }^{ 2} { x }^{ 2}\end{eqnarray}$$
$$ \left( { 1 - { e }^{ 2}} \right) { x }^{ 2} + { y }^{ 2} + 2 p e x - { p }^{ 2} = 0$$

If eccentricity $ e$ goes to zero we get a circular orbit.

$$ r = p = \frac{ { h }^{ 2}}{ \mu }$$

Let's now look at the case $ e \texttt{>} 0$ and $ e \texttt{<} 1$ (e.g. $ e = 0.02$ for the eccentricity of the earth around the sun). This gives us ellptical orbits.

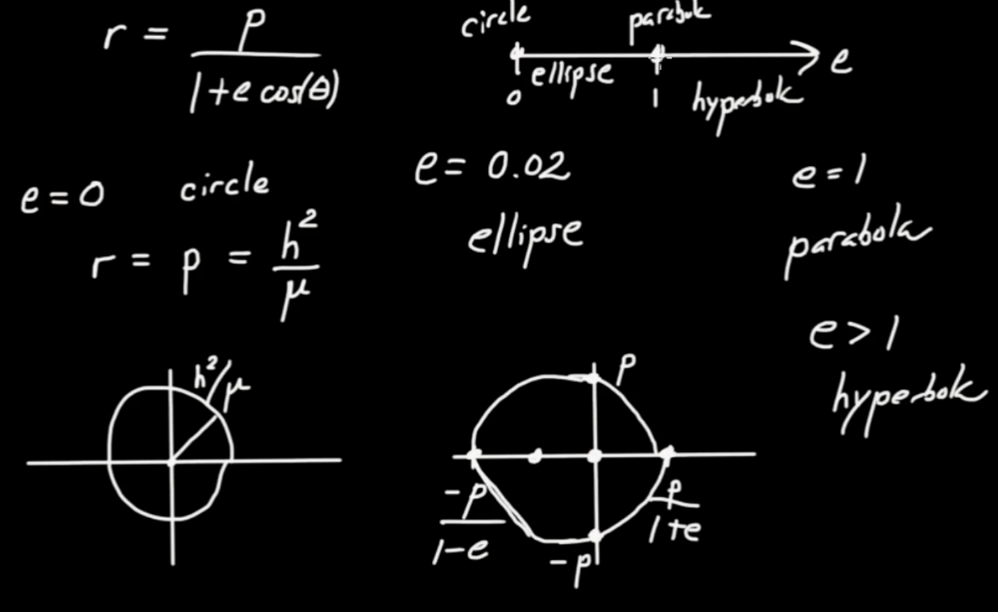If $ e$ becomes 1 we get the parabolic case.

If $ e$ becomes greater than 1 we get the hyperbolic case.

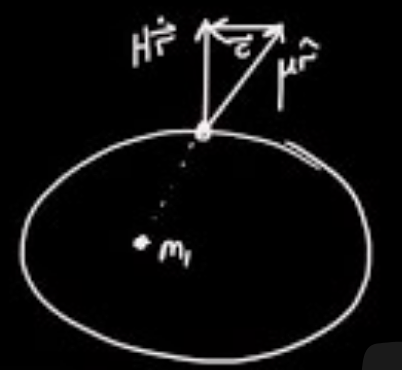
Let's have a detailed look on the conserved vector quantity.

$$ \vec{c} = H \dot{\vec{r}} - \mu { \vec{e} }_{ r}$$

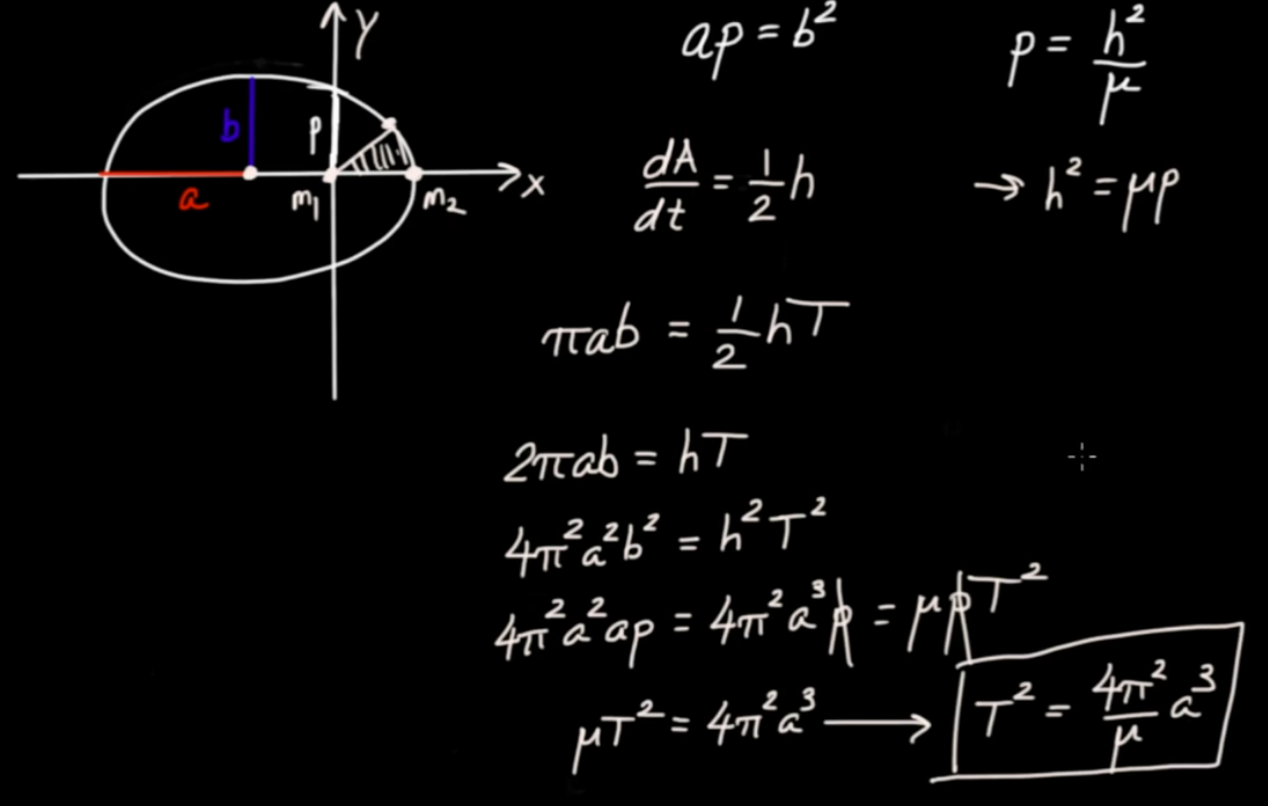
With Eq. 3 we have

$$ H = \vec{r} \wedge \dot{\vec{r}} = { r }^{ 2} { \vec{e} }_{ r} { \dot{\vec{e}} }_{ r} \qquad \mbox{Conserved angular momentum}$$

and thus

$$\begin{eqnarray} H \dot{\vec{r}} &=& { r }^{ 2} { \vec{e} }_{ r} { \dot{\vec{e}} }_{ r} \dot{\vec{r}} \\ H \dot{\vec{r}} &=& { r }^{ 2} { \vec{e} }_{ r} r \\ H \dot{\vec{r}} &=& { r }^{ 3} { \vec{e} }_{ r}\end{eqnarray}$$...

So far we have seen that the force law

$$ \ddot{\vec{r}} = - \frac{ \mu }{ { r }^{ 2}} { \vec{e} }_{ r}$$ with $$ \mu = \gamma \left( { { m }_{ 1} + { m }_{ 2}} \right)$$

leads to the following expressiom for the distance of both celstial bodies.

$$\begin{eqnarray} p &=& \frac{ { h }^{ 2}}{ \mu } \qquad \mbox{semi latus rectum} \\ e &=& \frac{ c}{ \mu } \qquad \mbox{eccentricity} \\ r \left( {\theta } \right) &=& \frac{ p}{ 1 + e \cos { \theta } } \qquad \mbox{radius of the orbit}\end{eqnarray}$$
with $ h = \left| { H} \right|$ being the magnitude of the conserved angular momentum and $ c = \left| { \vec{c}} \right|$ being the magnitud of the conserved vector quantity.

$$ H = \vec{r} \wedge \dot{\vec{r}} = { r }^{ 2} { \vec{e} }_{ r} { \dot{\vec{e}} }_{ r} \qquad \mbox{Conserved angular momentum}$$

$$ \vec{c} = H \dot{\vec{r}} - \mu { \vec{e} }_{ r} \qquad \mbox{Conserved vector quantity}$$

Geometric Algebra in 3D

Review of 2D

• associativity
• distributivity
• vector squared = magnitude of vector squared

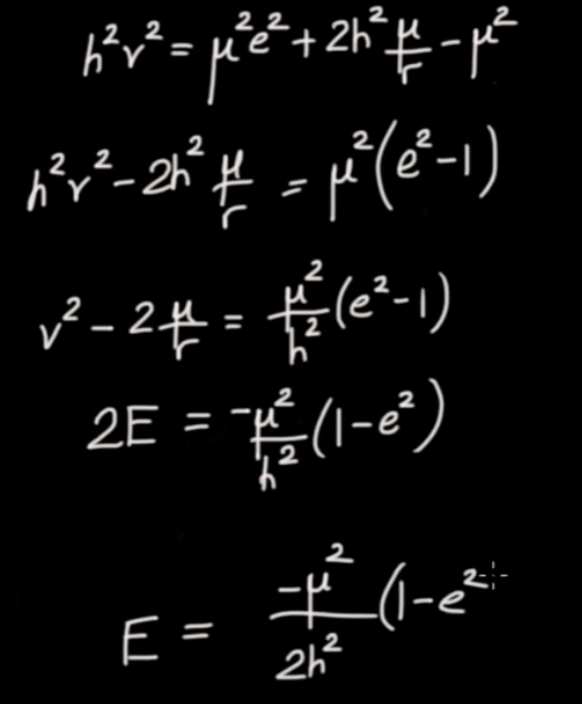$$\fbox{$ \displaystyle \vec{u} \cdot \vec{v} = \frac{ 1}{ 2} \left( { \vec{u} \vec{v} + \vec{v} \vec{u}} \right) $} \qquad \mbox{Scalar Product (generates a scalar)}$$

$$\fbox{$ \displaystyle \vec{u} \wedge \vec{v} = \frac{ 1}{ 2} \left( { \vec{u} \vec{v} - \vec{v} \vec{u}} \right) $} \qquad \mbox{Wedge Product (generates a bivector)}$$

The geometric product of multivectors generates another multivector which in the general case is a linear combination of all elements of the vector space.

$$ \vec{u} \vec{v} = \vec{u} \cdot \vec{v} + \vec{u} \wedge \vec{v}$$

The wedge product of two vectors anti-commutes. This implies that the geometric product of two orthogonal vectors anti-commutes.

$$ \vec{u} \wedge \vec{v} = - \vec{v} \wedge \vec{u}$$

It also implies that the geometric product commutes for two parallel vectors.

Setting up the 3D vector space

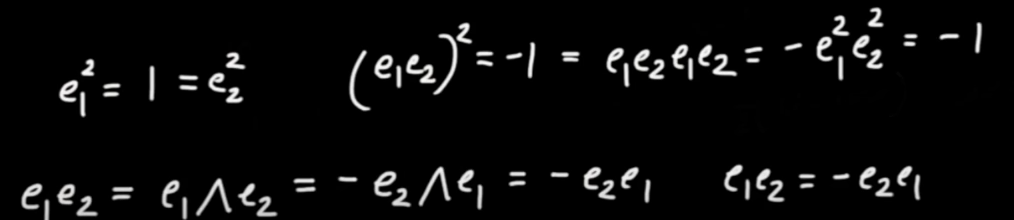$$ {\left( { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \right)}^{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} = { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 3} = - { \vec{e} }_{ 2} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 3} = - 1$$

We mutiply two arbitrary multi-vectors:

$$\begin{eqnarray} A B &=& \left( { 5 + 2 { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \left( { 2 + { \vec{e} }_{ 1} + { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3}} \right) \\ A B &=& 2 \left( { 5 + 2 { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) + \left( { 5 + 2 { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) { \vec{e} }_{ 1} + \left( { 5 + 2 { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \\ A B &=& \left( { 10 + 4 { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) + \left( { 5 { \vec{e} }_{ 1} + 2 { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1}} \right) + \left( { 5 { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + 2 { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3}} \right) \\ A B &=& 4 { \vec{e} }_{ 1} { \vec{e} }_{ 2} + 10 + 5 { \vec{e} }_{ 1} - 2 { \vec{e} }_{ 2} + 5 { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + 2 { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \\ A B &=& 10 + 5 { \vec{e} }_{ 1} - 2 { \vec{e} }_{ 2} + 5 { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} - 2 { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \\ A B &=& 10 + 5 { \vec{e} }_{ 1} - 2 { \vec{e} }_{ 2} + 5 { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} - 2 { \vec{e} }_{ 3} \\ A B &=& 10 + 5 { \vec{e} }_{ 1} - 2 { \vec{e} }_{ 2} - 2 { \vec{e} }_{ 3} + 5 { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3}\end{eqnarray}$$

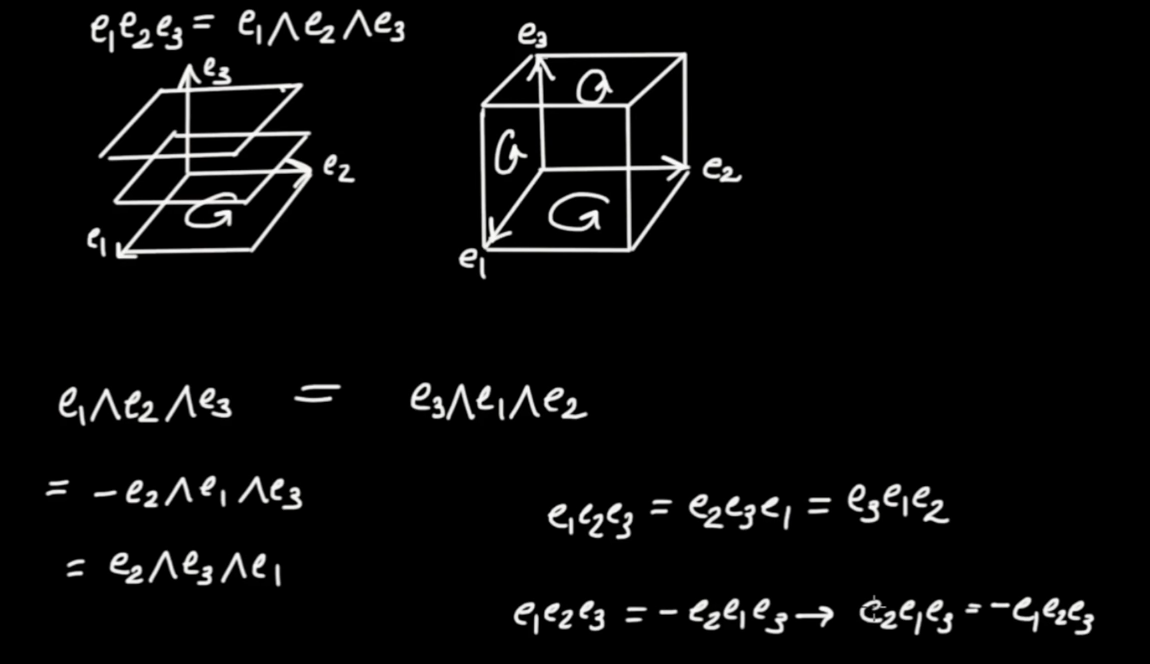Now that we have the elements of G(3)

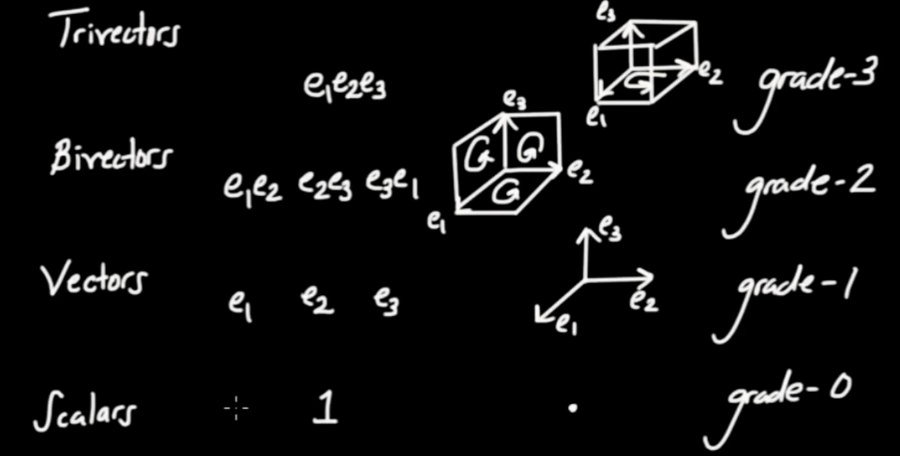we can check out what multiplication with the tri-vector does.

$$ \left( { { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \left( { { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3}} \right) = - { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} = - { \vec{e} }_{ 3}$$

$$ { \vec{e} }_{ 1} \left( { { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3}} \right) = { \vec{e} }_{ 2} { \vec{e} }_{ 3}$$

Multiplying a bi-vector generates a vector. Multiplying a vector generates a bi-vector and so on.

Geometric product of a vector and a vector

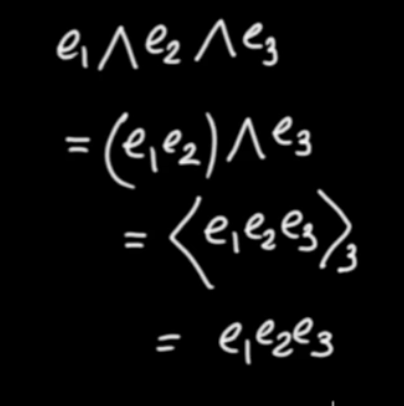$$ \vec{a} \vec{b} = \vec{a} \cdot \vec{b} + \vec{a} \wedge \vec{b}$$

$$\fbox{$ \displaystyle \vec{a} \cdot \vec{b} = { a }_{ x} { b }_{ x} + { a }_{ y} { b }_{ y} + { a }_{ z} { b }_{ z} $}$$

$$\fbox{$ \displaystyle \vec{a} \wedge \vec{b} = \left( { { a }_{ x} { b }_{ y} - { a }_{ y} { b }_{ x}} \right) { \vec{e} }_{ x} { \vec{e} }_{ y} + \left( { { a }_{ y} { b }_{ z} - { a }_{ z} { b }_{ y}} \right) { \vec{e} }_{ y} { \vec{e} }_{ z} + \left( { { a }_{ z} { b }_{ x} - { a }_{ x} { b }_{ z}} \right) { \vec{e} }_{ z} { \vec{e} }_{ x} $}$$

Geometric product of a vector with a bi-vector

$$ B = { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x}$$ $$ \vec{c} = { c }_{ x} { \vec{e} }_{ x} + { c }_{ y} { \vec{e} }_{ y} + { c }_{ z} { \vec{e} }_{ z}$$

$$\begin{eqnarray} B \vec{c} &=& \left( { { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x}} \right) \left( { { c }_{ x} { \vec{e} }_{ x} + { c }_{ y} { \vec{e} }_{ y} + { c }_{ z} { \vec{e} }_{ z}} \right) \\ B \vec{c} &=& { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} \left( { { c }_{ x} { \vec{e} }_{ x} + { c }_{ y} { \vec{e} }_{ y} + { c }_{ z} { \vec{e} }_{ z}} \right) + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} \left( { { c }_{ x} { \vec{e} }_{ x} + { c }_{ y} { \vec{e} }_{ y} + { c }_{ z} { \vec{e} }_{ z}} \right) + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} \left( { { c }_{ x} { \vec{e} }_{ x} + { c }_{ y} { \vec{e} }_{ y} + { c }_{ z} { \vec{e} }_{ z}} \right) \\ B \vec{c} &=& { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} { c }_{ x} { \vec{e} }_{ x} + { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} { c }_{ y} { \vec{e} }_{ y} + { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} { c }_{ z} { \vec{e} }_{ z} + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} { c }_{ x} { \vec{e} }_{ x} + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} { c }_{ y} { \vec{e} }_{ y} + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} { c }_{ z} { \vec{e} }_{ z} + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} { c }_{ x} { \vec{e} }_{ x} + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} { c }_{ y} { \vec{e} }_{ y} + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} { c }_{ z} { \vec{e} }_{ z} \\ B \vec{c} &=& - { B }_{ 1} { c }_{ x} { \vec{e} }_{ y} + { B }_{ 1} { c }_{ y} { \vec{e} }_{ x} + { B }_{ 1} { c }_{ z} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 2} { c }_{ x} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} - { B }_{ 2} { c }_{ y} { \vec{e} }_{ z} + { B }_{ 2} { c }_{ z} { \vec{e} }_{ y} + { B }_{ 3} { c }_{ x} { \vec{e} }_{ z} + { B }_{ 3} { c }_{ y} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} - { B }_{ 3} { c }_{ z} { \vec{e} }_{ x} \\ B \vec{c} &=& { B }_{ 1} { c }_{ y} { \vec{e} }_{ x} - { B }_{ 3} { c }_{ z} { \vec{e} }_{ x} + { B }_{ 2} { c }_{ z} { \vec{e} }_{ y} - { B }_{ 1} { c }_{ x} { \vec{e} }_{ y} - { B }_{ 2} { c }_{ y} { \vec{e} }_{ z} + { B }_{ 3} { c }_{ x} { \vec{e} }_{ z} + { B }_{ 3} { c }_{ y} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 2} { c }_{ x} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 1} { c }_{ z} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z}\end{eqnarray}$$
$$\fbox{$ \displaystyle B \vec{c} = \left( { { B }_{ 1} { c }_{ y} - { B }_{ 3} { c }_{ z}} \right) { \vec{e} }_{ x} + \left( { { B }_{ 2} { c }_{ z} - { B }_{ 1} { c }_{ x}} \right) { \vec{e} }_{ y} + \left( { { B }_{ 3} { c }_{ x} - { B }_{ 2} { c }_{ y}} \right) { \vec{e} }_{ z} + \left( { { B }_{ 1} { c }_{ z} + { B }_{ 2} { c }_{ x} + { B }_{ 3} { c }_{ y}} \right) { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} $}$$

$$\begin{eqnarray} \vec{c} B &=& \left( { { c }_{ x} { \vec{e} }_{ x} + { c }_{ y} { \vec{e} }_{ y} + { c }_{ z} { \vec{e} }_{ z}} \right) \left( { { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x}} \right) \\ \vec{c} B &=& \left( { { c }_{ x} { \vec{e} }_{ x} + { c }_{ y} { \vec{e} }_{ y} + { c }_{ z} { \vec{e} }_{ z}} \right) { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + \left( { { c }_{ x} { \vec{e} }_{ x} + { c }_{ y} { \vec{e} }_{ y} + { c }_{ z} { \vec{e} }_{ z}} \right) { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + \left( { { c }_{ x} { \vec{e} }_{ x} + { c }_{ y} { \vec{e} }_{ y} + { c }_{ z} { \vec{e} }_{ z}} \right) { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} \\ \vec{c} B &=& { c }_{ x} { \vec{e} }_{ x} { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { c }_{ y} { \vec{e} }_{ y} { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { c }_{ z} { \vec{e} }_{ z} { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { c }_{ x} { \vec{e} }_{ x} { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { c }_{ y} { \vec{e} }_{ y} { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { c }_{ z} { \vec{e} }_{ z} { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { c }_{ x} { \vec{e} }_{ x} { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} + { c }_{ y} { \vec{e} }_{ y} { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} + { c }_{ z} { \vec{e} }_{ z} { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} \\ \vec{c} B &=& { B }_{ 1} { c }_{ x} { \vec{e} }_{ y} - { B }_{ 1} { c }_{ y} { \vec{e} }_{ x} + { B }_{ 1} { c }_{ z} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 2} { c }_{ x} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 2} { c }_{ y} { \vec{e} }_{ z} - { B }_{ 2} { c }_{ z} { \vec{e} }_{ y} - { B }_{ 3} { c }_{ x} { \vec{e} }_{ z} + { B }_{ 3} { c }_{ y} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 3} { c }_{ z} { \vec{e} }_{ x} \\ \vec{c} B &=& { B }_{ 3} { c }_{ z} { \vec{e} }_{ x} - { B }_{ 1} { c }_{ y} { \vec{e} }_{ x} + { B }_{ 1} { c }_{ x} { \vec{e} }_{ y} - { B }_{ 2} { c }_{ z} { \vec{e} }_{ y} + { B }_{ 2} { c }_{ y} { \vec{e} }_{ z} - { B }_{ 3} { c }_{ x} { \vec{e} }_{ z} + { B }_{ 1} { c }_{ z} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 2} { c }_{ x} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 3} { c }_{ y} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z}\end{eqnarray}$$
$$\fbox{$ \displaystyle \vec{c} B = \left( { { B }_{ 3} { c }_{ z} - { B }_{ 1} { c }_{ y}} \right) { \vec{e} }_{ x} + \left( { { B }_{ 1} { c }_{ x} - { B }_{ 2} { c }_{ z}} \right) { \vec{e} }_{ y} + \left( { { B }_{ 2} { c }_{ y} - { B }_{ 3} { c }_{ x}} \right) { \vec{e} }_{ z} + \left( { { B }_{ 1} { c }_{ z} + { B }_{ 2} { c }_{ x} + { B }_{ 3} { c }_{ y}} \right) { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} $}$$

From these two results we get

$$ \langle B \vec{c}\rangle_{ 1} = - \langle \vec{c} B\rangle_{ 1}$$ $$\fbox{$ \displaystyle B \cdot \vec{c} \equiv \langle B \vec{c}\rangle_{ 1} $}$$

$$ \langle B \vec{c}\rangle_{ 3} = \langle \vec{c} B\rangle_{ 3}$$ $$\fbox{$ \displaystyle B \wedge \vec{c} \equiv \langle B \vec{c}\rangle_{ 3} $}$$

The result has a vector and a tri-vector part.

$$ \vec{a} = x { \vec{e} }_{ x} + y { \vec{e} }_{ y} + z { \vec{e} }_{ z}$$ $$ B = b { \vec{e} }_{ x} { \vec{e} }_{ y}$$

$$\begin{eqnarray} \vec{a} B &=& \left( { x { \vec{e} }_{ x} + y { \vec{e} }_{ y} + z { \vec{e} }_{ z}} \right) b { \vec{e} }_{ x} { \vec{e} }_{ y} \\ \vec{a} B &=& x { \vec{e} }_{ x} b { \vec{e} }_{ x} { \vec{e} }_{ y} + y { \vec{e} }_{ y} b { \vec{e} }_{ x} { \vec{e} }_{ y} + z { \vec{e} }_{ z} b { \vec{e} }_{ x} { \vec{e} }_{ y} \\ \vec{a} B &=& x b { \vec{e} }_{ x} { \vec{e} }_{ x} { \vec{e} }_{ y} + y b { \vec{e} }_{ y} { \vec{e} }_{ x} { \vec{e} }_{ y} + z b { \vec{e} }_{ z} { \vec{e} }_{ x} { \vec{e} }_{ y} \\ \vec{a} B &=& x b { \vec{e} }_{ y} - y b { \vec{e} }_{ x} + z b { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} \\ \vec{a} B &=& \langle \vec{a} B\rangle_{ 1} + \langle \vec{a} B\rangle_{ 3}\end{eqnarray}$$

$$ \langle \vec{a} B\rangle_{ 1} = x b { \vec{e} }_{ y} - y b { \vec{e} }_{ x}$$ $$ \langle \vec{a} B\rangle_{ 3} = z b { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z}$$

$$\begin{eqnarray} B \vec{a} &=& b { \vec{e} }_{ x} { \vec{e} }_{ y} \left( { x { \vec{e} }_{ x} + y { \vec{e} }_{ y} + z { \vec{e} }_{ z}} \right) \\ B \vec{a} &=& b { \vec{e} }_{ x} { \vec{e} }_{ y} x { \vec{e} }_{ x} + b { \vec{e} }_{ x} { \vec{e} }_{ y} y { \vec{e} }_{ y} + b { \vec{e} }_{ x} { \vec{e} }_{ y} z { \vec{e} }_{ z} \\ B \vec{a} &=& x b { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ x} + y b { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ y} + z b { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} \\ B \vec{a} &=& - x b { \vec{e} }_{ y} + y b { \vec{e} }_{ x} + z b { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} \\ B \vec{a} &=& \langle B \vec{a}\rangle_{ 1} + \langle B \vec{a}\rangle_{ 3}\end{eqnarray}$$
$$ \langle B \vec{a}\rangle_{ 1} = - x b { \vec{e} }_{ y} + y b { \vec{e} }_{ x}$$ $$ \langle B \vec{a}\rangle_{ 3} = z b { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z}$$

Comparing these two results gives us

$$ \langle \vec{a} B\rangle_{ 1} = - \langle B \vec{a}\rangle_{ 1}$$ $$ \langle \vec{a} B\rangle_{ 3} = \langle B \vec{a}\rangle_{ 3}$$

The grade-1 part anti-commutes and the grade-3 part commutes. For the product of two vectors we had found that the grade-0 part commutea and the grade-2 part anti-commutes. Interessting! We can now define the dot product of a vector with a bivector and the wedge product of a vector and a bi-vector like so.

$$\fbox{$ \displaystyle \vec{a} \cdot B = \langle \bar{a} B\rangle_{ 1} $} \qquad \mbox{Definition of the dot product of a vector and a bivector}$$

$$\fbox{$ \displaystyle \vec{a} \wedge B = \langle \bar{a} B\rangle_{ 3} $} \qquad \mbox{Definition of the wedge product of a vector and a bivector}$$

Since the geometric product of a vector and a bi-vector generates the sum of a grade-1 part and a grade-3 part

$$\begin{eqnarray} \vec{a} B &=& \langle \vec{a} B\rangle_{ 1} + \langle \vec{a} B\rangle_{ 3} \\ B \vec{a} &=& - \langle \vec{a} B\rangle_{ 1} + \langle \vec{a} B\rangle_{ 3}\end{eqnarray}$$

we can write using the above two definitions
$$ \vec{a} B = \vec{a} \cdot B + a \wedge B$$

We have seen that the gade-1 (dot product) of such a product anti-commutes and the that garde-3 part (wedge product) commutes.

$$ \vec{a} \cdot B = - B \cdot \vec{a}$$

$$ \vec{a} \wedge B = B \wedge \vec{a}$$

We therefore have

$$\begin{eqnarray} \vec{a} B + B \vec{a} &=& 2 \langle \vec{a} B\rangle_{ 3} \\ \vec{a} B - B \vec{a} &=& 2 \langle \vec{a} B\rangle_{ 1}\end{eqnarray}$$
and therefore

$$\fbox{$ \displaystyle \vec{a} \cdot B = \frac{ 1}{ 2} \left( { \vec{a} B - B \vec{a}} \right) $} \tag{4}$$
$$\fbox{$ \displaystyle \vec{a} \wedge B = \frac{ 1}{ 2} \left( { \vec{a} B + B \vec{a}} \right) $}$$

For two parallel vectors we have seen that the geometric product commutes since the wedge product is zero. And for two orthogonal vectors we have seen that the geometric product anti-commutes since the dot product is zero. We extend this consideration to the geometric product of a vector with a bi-vector.

Vector is co-planar to the bi-vector

$$ B = b { \vec{e} }_{ x} { \vec{e} }_{ y}$$ $$ \vec{a} = x { \vec{e} }_{ x} + y { \vec{e} }_{ y}$$
We then have

$$\begin{eqnarray} \vec{a} B &=& \left( { x { \vec{e} }_{ x} + y { \vec{e} }_{ y}} \right) b { \vec{e} }_{ x} { \vec{e} }_{ y} \\ \vec{a} B &=& x { \vec{e} }_{ x} b { \vec{e} }_{ x} { \vec{e} }_{ y} + y { \vec{e} }_{ y} b { \vec{e} }_{ x} { \vec{e} }_{ y} \\ \vec{a} B &=& x b { \vec{e} }_{ y} - y b { \vec{e} }_{ x} \\ \vec{a} B &=& - y b { \vec{e} }_{ x} + x b { \vec{e} }_{ y}\end{eqnarray}$$
The resulting vector lies also in the plane scaled by the magnitude of the bi-vector and rotated CCW by 90°.

We now consider an example in which the vector is orthogonal to the bi-vectors plane.

$$ B = b { \vec{e} }_{ x} { \vec{e} }_{ y}$$ $$ \vec{a} = z { \vec{e} }_{ z}$$

$$\begin{eqnarray} \vec{a} B &=& z { \vec{e} }_{ z} b { \vec{e} }_{ x} { \vec{e} }_{ y} \\ \vec{a} B &=& z b { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z}\end{eqnarray}$$
The result is a tri- with a magnitude given by the product of the magnitude of the bi-vector and that of the vector. We look at

$$\begin{eqnarray} B \vec{a} &=& b { \vec{e} }_{ x} { \vec{e} }_{ y} \left( { x { \vec{e} }_{ x} + y { \vec{e} }_{ y}} \right) \\ B \vec{a} &=& b { \vec{e} }_{ x} { \vec{e} }_{ y} x { \vec{e} }_{ x} + b { \vec{e} }_{ x} { \vec{e} }_{ y} y { \vec{e} }_{ y} \\ B \vec{a} &=& - b x { \vec{e} }_{ y} + b y { \vec{e} }_{ x} \\ B \vec{a} &=& y b { \vec{e} }_{ x} - x b { \vec{e} }_{ y}\end{eqnarray}$$
and by comapring with the calculation above realize that

$$\fbox{$ \displaystyle \vec{a} B = - B \vec{a} $} \qquad \mbox{if vector lies in the plane of the bi-vector}$$

so the geometric product of a vector with a bi-vector anti-commutes.

We produce a different and more general proof that the the product of a vector with a bi-vector anti-commutes if the vector lies in the plane of the bi-vector. For that we define

$$ B = \vec{u} \wedge \vec{v}$$ $$ \vec{a} = \gamma \vec{u} + \eta \vec{v}$$

But before actually considering the product $ \vec{a} B$ we first checkout the products $ \vec{u} B$ and $ \vec{v} B$. This will help us when later looking atthe more general case. We have

$$\begin{eqnarray} \vec{u} B &=& \vec{u} \left( { \vec{u} \wedge \vec{v}} \right) \\ \vec{u} B &=& \vec{u} \frac{ 1}{ 2} \left( { \vec{u} \vec{v} - \vec{v} \vec{u}} \right) \\ \vec{u} B &=& \frac{ 1}{ 2} \left( { \vec{u} \vec{u} \vec{v} - \vec{u} \vec{v} \vec{u}} \right) \\ \vec{u} B &=& \frac{ 1}{ 2} \left( { { \left| { \vec{u}} \right| }^{ 2} \vec{v} - \vec{u} \vec{v} \vec{u}} \right) \\ \vec{u} B &=& \frac{ 1}{ 2} \left( { \vec{v} { \left| { \vec{u}} \right| }^{ 2} - \vec{u} \vec{v} \vec{u}} \right) \\ \vec{u} B &=& \frac{ 1}{ 2} \left( { \vec{v} \vec{u} \vec{u} - \vec{u} \vec{v} \vec{u}} \right) \\ \vec{u} B &=& \frac{ 1}{ 2} \left( { \vec{v} \vec{u} - \vec{u} \vec{v}} \right) \vec{u} \\ \vec{u} B &=& \left( { \vec{v} \wedge \vec{u}} \right) \vec{u} \\ \vec{u} B &=& - \left( { \vec{u} \wedge \vec{v}} \right) \vec{u} \\ \vec{u} B &=& - \vec{B} \vec{u}\end{eqnarray}$$
We likewise get

$$\begin{eqnarray} \vec{v} B &=& \vec{v} \left( { \vec{u} \wedge \vec{v}} \right) \\ \vec{v} B &=& \vec{v} \frac{ 1}{ 2} \left( { \vec{u} \vec{v} - \vec{v} \vec{u}} \right) \\ \vec{v} B &=& \frac{ 1}{ 2} \left( { \vec{v} \vec{u} \vec{v} - \vec{v} \vec{v} \vec{u}} \right) \\ \vec{v} B &=& \frac{ 1}{ 2} \left( { \vec{v} \vec{u} \vec{v} - \vec{u} \vec{v} \vec{v}} \right) \\ \vec{v} B &=& \frac{ 1}{ 2} \left( { \vec{v} \vec{u} - \vec{u} \vec{v}} \right) \vec{v} \\ \vec{v} B &=& \left( { \vec{v} \wedge \vec{u}} \right) \vec{v} \\ \vec{v} B &=& - \left( { \vec{u} \wedge \vec{v}} \right) \vec{v} \\ \vec{v} B &=& - B \vec{v}\end{eqnarray}$$We are now prepared to look at the general case.

$$\begin{eqnarray} \vec{a} \vec{B} &=& \left( { \gamma \vec{u} + \eta \vec{v}} \right) B \\ \vec{a} \vec{B} &=& \gamma \vec{u} B + \eta \vec{v} B \\ \vec{a} \vec{B} &=& - \gamma B \vec{u} - \eta B \vec{v} \\ \vec{a} \vec{B} &=& - B \left( { \gamma \vec{u} + \eta \vec{v}} \right)\end{eqnarray}$$
$$\fbox{$ \displaystyle \vec{a} \vec{B} = - B \vec{a} $} \qquad \mbox{if vector lies in the plane of the bi-vector}$$

This anti-commutativity also means

$$\begin{eqnarray} \vec{a} B + B \vec{a} &=& 0 \\ \frac{ 1}{ 2} \left( { \vec{a} B + B \vec{a}} \right) &=& 0\end{eqnarray}$$
$$\fbox{$ \displaystyle \vec{a} \wedge B = 0 $} \qquad \mbox{for a co-planar vector}$$

Let's show that vector $ \vec{a} ' = \vec{a} B$ lies in the plane B if $ \vec{a}$ lies in the plane.

$$ \vec{a'} = \vec{a} B$$
Lying in the plane means $ \vec{a'} = \alpha \vec{u} + \beta \vec{v}$. Let's see.

$$\begin{eqnarray} \vec{a'} &=& \left( { \gamma \vec{u} + \eta \vec{v}} \right) B \\ \vec{a'} &=& \gamma \vec{u} B + \eta \vec{v} B \\ \vec{a'} &=& \gamma \vec{u} B - \eta B \vec{v} \\ \vec{a'} &=& \gamma \vec{u} \left( { \vec{u} \wedge \vec{v}} \right) - \eta \left( { \vec{u} \wedge \vec{v}} \right) \vec{v} \\ \vec{a'} &=& \gamma \vec{u} \frac{ 1}{ 2} \left( { \vec{u} \vec{v} - \vec{v} \vec{u}} \right) - \eta \frac{ 1}{ 2} \left( { \vec{u} \vec{v} - \vec{v} \vec{u}} \right) \vec{v} \\ \vec{a'} &=& \gamma \vec{u} \frac{ 1}{ 2} \left( { \vec{u} \vec{v} - \vec{v} \vec{u}} \right) - \eta \frac{ 1}{ 2} \left( { \vec{u} \vec{v} - \vec{v} \vec{u}} \right) \vec{v} \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \gamma \vec{u} \vec{u} \vec{v} - \gamma \vec{u} \vec{v} \vec{u}} \right) - \frac{ 1}{ 2} \left( { \eta \vec{u} \vec{v} \vec{v} - \eta \vec{v} \vec{u} \vec{v}} \right) \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \gamma \vec{u} \vec{u} \vec{v} - \gamma \vec{u} \vec{v} \vec{u} - \eta \vec{u} \vec{v} \vec{v} + \eta \vec{v} \vec{u} \vec{v}} \right) \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \gamma \vec{u} \vec{u} \vec{v} + \eta \vec{v} \vec{u} \vec{v} - \vec{u} \left( { \eta \vec{v} \vec{v} + \gamma \vec{v} \vec{u}} \right)} \right) \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \left( { \gamma \vec{u} \vec{u} + \eta \vec{v} \vec{u}} \right) \vec{v} - \vec{u} \left( { \eta \vec{v} \vec{v} + \gamma \vec{v} \vec{u}} \right)} \right) \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \left( { \gamma \vec{u} \vec{u} + \eta \left( { \vec{v} \cdot \vec{u} + \vec{v} \wedge \vec{u}} \right)} \right) \vec{v} - \vec{u} \left( { \eta \vec{v} \vec{v} + \gamma \left( { \vec{v} \cdot \vec{u} + \vec{v} \wedge \vec{u}} \right)} \right)} \right) \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \left( { \gamma \vec{u} \vec{u} + \eta \left( { \vec{v} \cdot \vec{u} - B} \right)} \right) \vec{v} - \vec{u} \left( { \eta \vec{v} \vec{v} + \gamma \left( { \vec{v} \cdot \vec{u} - B} \right)} \right)} \right) \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} \vec{v} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \vec{v} - \eta B \vec{v} - \left( { \eta { \left| { \vec{v}} \right| }^{ 2} \vec{u} + \gamma \left( { \vec{v} \cdot \vec{u}} \right) \vec{u} - \gamma \vec{u} B} \right)} \right) \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} \vec{v} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \vec{v} - \eta B \vec{v} - \eta { \left| { \vec{v}} \right| }^{ 2} \vec{u} - \gamma \left( { \vec{v} \cdot \vec{u}} \right) \vec{u} + \gamma \vec{u} B} \right) \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} \vec{v} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \vec{v} - \eta B \vec{v} - \eta { \left| { \vec{v}} \right| }^{ 2} \vec{u} - \gamma \left( { \vec{v} \cdot \vec{u}} \right) \vec{u} + \gamma \vec{u} B} \right) \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} \vec{v} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \vec{v} + \eta \vec{v} B - \eta { \left| { \vec{v}} \right| }^{ 2} \vec{u} - \gamma \left( { \vec{v} \cdot \vec{u}} \right) \vec{u} + \gamma \vec{u} B} \right) \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} \vec{v} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \vec{v} - \eta { \left| { \vec{v}} \right| }^{ 2} \vec{u} - \gamma \left( { \vec{v} \cdot \vec{u}} \right) \vec{u} + \left( { \eta \vec{v} + \gamma \vec{u}} \right) B} \right) \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} \vec{v} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \vec{v} - \eta { \left| { \vec{v}} \right| }^{ 2} \vec{u} - \gamma \left( { \vec{v} \cdot \vec{u}} \right) \vec{u} + \vec{a'}} \right) \\ \vec{a'} &=& \frac{ 1}{ 2} \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} \vec{v} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \vec{v} - \eta { \left| { \vec{v}} \right| }^{ 2} \vec{u} - \gamma \left( { \vec{v} \cdot \vec{u}} \right) \vec{u}} \right) + \frac{ 1}{ 2} \vec{a'} \\ \frac{ 1}{ 2} \vec{a'} &=& \frac{ 1}{ 2} \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} \vec{v} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \vec{v} - \eta { \left| { \vec{v}} \right| }^{ 2} \vec{u} - \gamma \left( { \vec{v} \cdot \vec{u}} \right) \vec{u}} \right) \\ \vec{a'} &=& \gamma { \left| { \vec{u}} \right| }^{ 2} \vec{v} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \vec{v} - \eta { \left| { \vec{v}} \right| }^{ 2} \vec{u} - \gamma \left( { \vec{v} \cdot \vec{u}} \right) \vec{u} \\ \vec{a'} &=& \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{v} - \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{u}\end{eqnarray}$$
$$\fbox{$ \displaystyle \vec{a'} = - \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{u} + \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{v} $}$$

We have thus shown that $ \vec{a'}$ lies in the plane spanned by $ \vec{u}$ and $ \vec{v}$. And we have also calculated the factors

$$ \alpha = - \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right)$$ $$ \beta = \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \qquad \mbox{not yet verified}$$

for the rotation performed by $ \vec{a'} = \vec{a} B$ with $ B = \vec{u} \wedge \vec{v}$.

Proof of 90° rotation
Now that we have the components of $ \vec{a'}$ we can show that the multiplication performs a 90° rotation.

$$\begin{eqnarray} \vec{a} \wedge \vec{a'} &=& - \vec{a'} \wedge \vec{a} \\ \vec{a} \vec{a'} &=& - \vec{a'} \vec{a}\end{eqnarray}$$

$$\begin{eqnarray} \left( { \gamma \vec{u} + \eta \vec{v}} \right) \left( { - \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{u} + \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{v}} \right) &=& - \left( { - \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{u} + \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{v}} \right) \left( { \gamma \vec{u} + \eta \vec{v}} \right) \\ \left( { \gamma \vec{u} + \eta \vec{v}} \right) \left( { - \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{u} + \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{v}} \right) &=& \left( { \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{u} - \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{v}} \right) \left( { \gamma \vec{u} + \eta \vec{v}} \right) \\ - \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) \left( { \gamma \vec{u} + \eta \vec{v}} \right) \vec{u} + \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \left( { \gamma \vec{u} + \eta \vec{v}} \right) \vec{v} &=& \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{u} \left( { \gamma \vec{u} + \eta \vec{v}} \right) - \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \vec{v} \left( { \gamma \vec{u} + \eta \vec{v}} \right) \\ - \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) \left( { \gamma { \vec{u} }^{ 2} + \eta \vec{v} \vec{u}} \right) + \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \left( { \gamma \vec{u} \vec{v} + \eta { \vec{v} }^{ 2}} \right) &=& \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) \left( { \gamma { \vec{u} }^{ 2} + \eta \vec{u} \vec{v}} \right) - \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \left( { \gamma \vec{v} \vec{u} + \eta { \vec{v} }^{ 2}} \right) \\ \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) \left( { - \gamma { \vec{u} }^{ 2} - \eta \vec{v} \vec{u}} \right) + \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \left( { \gamma \vec{u} \vec{v} + \eta { \vec{v} }^{ 2}} \right) &=& \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) \left( { \gamma { \vec{u} }^{ 2} + \eta \vec{u} \vec{v}} \right) - \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \left( { \gamma \vec{v} \vec{u} + \eta { \vec{v} }^{ 2}} \right)\end{eqnarray}$$...

If that is the case the scalar product $ \vec{a} \cdot \vec{a'}$ should be zero.
$$\begin{eqnarray} \vec{a} \cdot \vec{a'} &=& \frac{ 1}{ 2} \left( { \vec{a} \vec{a'} + \vec{a'} \vec{a}} \right) \\ \vec{a} \cdot \vec{a'} &=& \frac{ 1}{ 2} \left( { \left( { \gamma \vec{u} + \eta \vec{v}} \right) \left( { \alpha \vec{u} + \beta \vec{v}} \right) + \left( { \alpha \vec{u} + \beta \vec{v}} \right) \left( { \gamma \vec{u} + \eta \vec{v}} \right)} \right) \\ \vec{a} \cdot \vec{a'} &=& \frac{ 1}{ 2} \left( { \left( { \alpha \left( { \gamma \vec{u} + \eta \vec{v}} \right) \vec{u} + \beta \left( { \gamma \vec{u} + \eta \vec{v}} \right) \vec{v}} \right) + \left( { \gamma \left( { \alpha \vec{u} + \beta \vec{v}} \right) \vec{u} + \eta \left( { \alpha \vec{u} + \beta \vec{v}} \right) \vec{v}} \right)} \right) \\ \vec{a} \cdot \vec{a'} &=& \frac{ 1}{ 2} \left( { \left( { \left( { \alpha \gamma \vec{u} + \alpha \eta \vec{v}} \right) \vec{u} + \left( { \beta \gamma \vec{u} + \beta \eta \vec{v}} \right) \vec{v}} \right) + \left( { \left( { \alpha \gamma \vec{u} + \beta \gamma \vec{v}} \right) \vec{u} + \left( { \alpha \eta \vec{u} + \beta \eta \vec{v}} \right) \vec{v}} \right)} \right) \\ \vec{a} \cdot \vec{a'} &=& \frac{ 1}{ 2} \left( { \left( { \left( { \alpha \gamma \vec{u} \vec{u} + \alpha \eta \vec{v} \vec{u}} \right) + \left( { \beta \gamma \vec{u} \vec{v} + \beta \eta \vec{v} \vec{v}} \right)} \right) + \left( { \left( { \alpha \gamma \vec{u} \vec{u} + \beta \gamma \vec{v} \vec{u}} \right) + \left( { \alpha \eta \vec{u} \vec{v} + \beta \eta \vec{v} \vec{v}} \right)} \right)} \right) \\ \vec{a} \cdot \vec{a'} &=& \frac{ 1}{ 2} \left( { \alpha \gamma { \vec{u} }^{ 2} + \alpha \eta \vec{v} \vec{u} + \beta \gamma \vec{u} \vec{v} + \beta \eta { \vec{v} }^{ 2} + \alpha \gamma { \vec{u} }^{ 2} + \beta \gamma \vec{v} \vec{u} + \alpha \eta \vec{u} \vec{v} + \beta \eta { \vec{v} }^{ 2}} \right) \\ \vec{a} \cdot \vec{a'} &=& \frac{ 1}{ 2} \left( { 2 \alpha \gamma { \vec{u} }^{ 2} + \alpha \eta \vec{v} \vec{u} + \beta \gamma \vec{v} \vec{u} + \beta \gamma \vec{u} \vec{v} + \alpha \eta \vec{u} \vec{v} + 2 \beta \eta { \vec{v} }^{ 2}} \right) \\ \vec{a} \cdot \vec{a'} &=& \frac{ 1}{ 2} \left( { 2 \alpha \gamma { \vec{u} }^{ 2} + \left( { \alpha \eta + \beta \gamma } \right) \vec{v} \vec{u} + \left( { \beta \gamma + \alpha \eta } \right) \vec{u} \vec{v} + 2 \beta \eta { \vec{v} }^{ 2}} \right) \\ \vec{a} \cdot \vec{a'} &=& \frac{ 1}{ 2} \left( { 2 \alpha \gamma { \vec{u} }^{ 2} + \left( { \alpha \eta + \beta \gamma } \right) \vec{v} \vec{u} + \left( { \alpha \eta + \beta \gamma } \right) \vec{u} \vec{v} + 2 \beta \eta { \vec{v} }^{ 2}} \right) \\ \vec{a} \cdot \vec{a'} &=& \frac{ 1}{ 2} \left( { 2 \alpha \gamma { \vec{u} }^{ 2} + \left( { \alpha \eta + \beta \gamma } \right) \left( { \vec{u} \vec{v} + \vec{v} \vec{u}} \right) + 2 \beta \eta { \vec{v} }^{ 2}} \right) \\ \vec{a} \cdot \vec{a'} &=& \frac{ 1}{ 2} \left( { 2 \alpha \gamma { \vec{u} }^{ 2} + 2 \left( { \alpha \eta + \beta \gamma } \right) \left( { \vec{u} \cdot \vec{v}} \right) + 2 \beta \eta { \vec{v} }^{ 2}} \right) \\ \vec{a} \cdot \vec{a'} &=& \alpha \gamma { \vec{u} }^{ 2} + \left( { \alpha \eta + \beta \gamma } \right) \left( { \vec{u} \cdot \vec{v}} \right) + \beta \eta { \vec{v} }^{ 2} \\ \vec{a} \cdot \vec{a'} &=& \alpha \gamma { \vec{u} }^{ 2} + \left( { \alpha \eta + \beta \gamma } \right) \left( { \vec{u} \cdot \vec{v}} \right) + \beta \eta { \vec{v} }^{ 2}\end{eqnarray}$$

We now substitute our values for $ \alpha $ and $ \beta $.

$$\begin{eqnarray} \vec{a} \cdot \vec{a'} &=& \left( { - \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right)} \right) \gamma { \vec{u} }^{ 2} + \left( { \left( { - \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right)} \right) \eta + \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \gamma } \right) \left( { \vec{u} \cdot \vec{v}} \right) + \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \eta { \vec{v} }^{ 2} \\ \vec{a} \cdot \vec{a'} &=& - \gamma { \vec{u} }^{ 2} \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) + \left( { - \left( { { \eta }^{ 2} { \left| { \vec{v}} \right| }^{ 2} + \gamma \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) + \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \gamma } \right) \left( { \vec{u} \cdot \vec{v}} \right) + \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right)} \right) \eta { \vec{v} }^{ 2} \\ \vec{a} \cdot \vec{a'} &=& - \gamma { \vec{u} }^{ 2} \left( { \eta { \left| { \vec{v}} \right| }^{ 2} + \gamma \left( { \vec{v} \cdot \vec{u}} \right)} \right) - { \eta }^{ 2} { \left| { \vec{v}} \right| }^{ 2} - \gamma \eta \left( { \vec{v} \cdot \vec{u}} \right) + \left( { \left( { { \gamma }^{ 2} { \left| { \vec{u}} \right| }^{ 2} \vec{u}} \right) \cdot \vec{v} + \gamma \eta {\left( \vec{v} \cdot \vec{u} \right)}^{ 2}} \right) + \left( { \gamma { \left| { \vec{u}} \right| }^{ 2} \eta { \vec{v} }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \eta { \vec{v} }^{ 2}} \right) \\ \vec{a} \cdot \vec{a'} &=& - \gamma { \vec{u} }^{ 2} \eta { \left| { \vec{v}} \right| }^{ 2} - \gamma { \vec{u} }^{ 2} \gamma \left( { \vec{v} \cdot \vec{u}} \right) - { \eta }^{ 2} { \left| { \vec{v}} \right| }^{ 2} - \gamma \eta \left( { \vec{v} \cdot \vec{u}} \right) + { \gamma }^{ 2} { \left| { \vec{u}} \right| }^{ 2} \left( { \vec{u} \cdot \vec{v}} \right) + \gamma \eta {\left( \vec{v} \cdot \vec{u} \right)}^{ 2} + \gamma { \left| { \vec{u}} \right| }^{ 2} \eta { \vec{v} }^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \eta { \vec{v} }^{ 2} \\ \vec{a} \cdot \vec{a'} &=& - { \eta }^{ 2} { \left| { \vec{v}} \right| }^{ 2} - \gamma \eta \left( { \vec{v} \cdot \vec{u}} \right) + \gamma \eta {\left( \vec{v} \cdot \vec{u} \right)}^{ 2} + \eta \left( { \vec{v} \cdot \vec{u}} \right) \eta { \vec{v} }^{ 2} \\ \vec{a} \cdot \vec{a'} &=& - { \eta }^{ 2} { \left| { \vec{v}} \right| }^{ 2} - \gamma \eta \left( { \vec{v} \cdot \vec{u}} \right) + \gamma \eta {\left( \vec{v} \cdot \vec{u} \right)}^{ 2} + { \eta }^{ 2} \left( { \vec{v} \cdot \vec{u}} \right) { \vec{v} }^{ 2}\end{eqnarray}$$
...

Vector is orthogonal to bi-vector

$$ B = b { \vec{e} }_{ x} { \vec{e} }_{ y}$$ $$ \vec{w} = z { \vec{e} }_{ z}$$

$$\begin{eqnarray} \vec{w} B &=& z { \vec{e} }_{ z} b { \vec{e} }_{ x} { \vec{e} }_{ y} \\ \vec{w} B &=& z b { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z}\end{eqnarray}$$
$$\begin{eqnarray} B \vec{w} &=& b { \vec{e} }_{ x} { \vec{e} }_{ y} z { \vec{e} }_{ z} \\ B \vec{w} &=& z b { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z}\end{eqnarray}$$

$$\fbox{$ \displaystyle B \vec{w} = B \vec{w} $} \qquad \mbox{if vector is orthogonal to bi-vector}$$

We add another more general proof for this.

$$\begin{eqnarray} \vec{w} B &=& \vec{w} \left( { \vec{u} \wedge \vec{v}} \right) \\ \vec{w} B &=& \vec{w} \frac{ 1}{ 2} \left( { \vec{u} \vec{v} - \vec{v} \vec{u}} \right) \\ \vec{w} B &=& \frac{ 1}{ 2} \left( { \vec{w} \vec{u} \vec{v} - \vec{w} \vec{v} \vec{u}} \right)\end{eqnarray}$$
Since $ \vec{w}$ is per definition orthogonal to $ \vec{u}$ and $ \vec{v}$ the vectors anti-commute if swapped.

$$\begin{eqnarray} \vec{w} B &=& \frac{ 1}{ 2} \left( { - \vec{u} \vec{w} \vec{v} + \vec{v} \vec{w} \vec{u}} \right) \\ \vec{w} B &=& \frac{ 1}{ 2} \left( { \vec{u} \vec{v} \vec{w} - \vec{v} \vec{u} \vec{w}} \right) \\ \vec{w} B &=& \frac{ 1}{ 2} \left( { \vec{u} \vec{v} - \vec{v} \vec{u}} \right) \vec{w} \\ \vec{w} B &=& \left( { \vec{u} \wedge \vec{v}} \right) \vec{w}\end{eqnarray}$$

$$\fbox{$ \displaystyle \vec{w} B = B \vec{w} $} \qquad \mbox{if vector is orthogonal to the plane of the bi-vector}$$

This also means

$$\begin{eqnarray} \vec{w} B - B \vec{w} &=& 0 \\ \frac{ 1}{ 2} \left( { \vec{w} B - B \vec{w}} \right) &=& 0\end{eqnarray}$$

$$\fbox{$ \displaystyle \vec{w} \cdot B = 0 $} \qquad \mbox{for an orthogonal vector}$$

General vector with respect to bi-vector

$$ \vec{b} = \vec{a} + \vec{w}$$

with a co-planar component $ \vec{a}$ and an orthogonal component $ \vec{w}$. What do we get for the scalar product $ \vec{b} \cdot B$?

$$\begin{eqnarray} \vec{b} \cdot B &=& \left( { \vec{a} + \vec{w}} \right) \cdot B \\ \vec{b} \cdot B &=& \vec{a} \cdot B + \vec{w} \cdot B \\ \vec{b} \cdot B &=& \vec{a} \cdot B + \vec{w} \cdot B\end{eqnarray}$$
$$\fbox{$ \displaystyle \vec{b} \cdot B = \vec{a} \cdot B = \vec{a} B $}$$

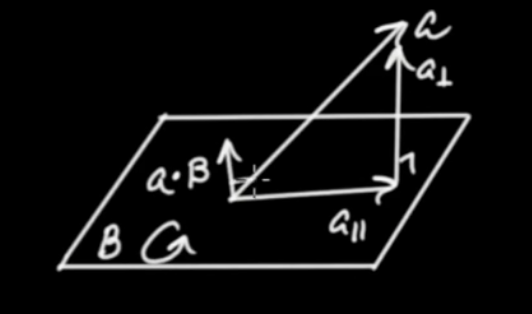The dot product $ \vec{b} \cdot B$ projects $ \vec{b}$ onto $ B$ and then rotates it by 90° in the diretion of the bi-vector and scales it by the magnitude of $ B$.

$$\begin{eqnarray} \vec{b} \wedge B &=& \left( { \vec{a} + \vec{w}} \right) \wedge B \\ \vec{b} \wedge B &=& \vec{a} \wedge B + \vec{w} \wedge B\end{eqnarray}$$
$$\fbox{$ \displaystyle \vec{b} \wedge B = \vec{w} \wedge B = \vec{w} B $}$$

The wedge product generates an oriented volume with the orthogonal component of the vector.

Geometric product of a bi-vector with a bi-vector

$$ B = { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x}$$ $$ C = { C }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { C }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { C }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x}$$

$$\begin{eqnarray} B C &=& \left( { { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x}} \right) \left( { { C }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { C }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { C }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x}} \right) \\ B C &=& { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} \left( { { C }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { C }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { C }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x}} \right) + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} \left( { { C }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { C }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { C }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x}} \right) + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} \left( { { C }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { C }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { C }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x}} \right) \\ B C &=& { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} { C }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} { C }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} { C }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} { C }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} { C }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} { C }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} { C }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} { C }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} { C }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} \\ B C &=& { B }_{ 1} { C }_{ 1} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ x} { \vec{e} }_{ y} + { B }_{ 1} { C }_{ 2} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 1} { C }_{ 3} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} { \vec{e} }_{ x} + { B }_{ 2} { C }_{ 1} { \vec{e} }_{ y} { \vec{e} }_{ z} { \vec{e} }_{ x} { \vec{e} }_{ y} + { B }_{ 2} { C }_{ 2} { \vec{e} }_{ y} { \vec{e} }_{ z} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 2} { C }_{ 3} { \vec{e} }_{ y} { \vec{e} }_{ z} { \vec{e} }_{ z} { \vec{e} }_{ x} + { B }_{ 3} { C }_{ 1} { \vec{e} }_{ z} { \vec{e} }_{ x} { \vec{e} }_{ x} { \vec{e} }_{ y} + { B }_{ 3} { C }_{ 2} { \vec{e} }_{ z} { \vec{e} }_{ x} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 3} { C }_{ 3} { \vec{e} }_{ z} { \vec{e} }_{ x} { \vec{e} }_{ z} { \vec{e} }_{ x} \\ B C &=& - { B }_{ 1} { C }_{ 1} + { B }_{ 1} { C }_{ 2} { \vec{e} }_{ x} { \vec{e} }_{ z} + { B }_{ 1} { C }_{ 3} { \vec{e} }_{ y} { \vec{e} }_{ z} + { B }_{ 2} { C }_{ 1} { \vec{e} }_{ z} { \vec{e} }_{ x} - { B }_{ 2} { C }_{ 2} + { B }_{ 2} { C }_{ 3} { \vec{e} }_{ y} { \vec{e} }_{ x} + { B }_{ 3} { C }_{ 1} { \vec{e} }_{ z} { \vec{e} }_{ y} + { B }_{ 3} { C }_{ 2} { \vec{e} }_{ x} { \vec{e} }_{ y} - { B }_{ 3} { C }_{ 3} \\ B C &=& - { B }_{ 1} { C }_{ 1} - { B }_{ 2} { C }_{ 2} - { B }_{ 3} { C }_{ 3} + \left( { { B }_{ 2} { C }_{ 1} - { B }_{ 1} { C }_{ 2}} \right) { \vec{e} }_{ z} { \vec{e} }_{ x} + \left( { { B }_{ 1} { C }_{ 3} - { B }_{ 3} { C }_{ 1}} \right) { \vec{e} }_{ y} { \vec{e} }_{ z} + \left( { { B }_{ 3} { C }_{ 2} - { B }_{ 2} { C }_{ 3}} \right) { \vec{e} }_{ x} { \vec{e} }_{ y}\end{eqnarray}$$
We end up with a scalar and a bi-vector component.

Addition of bi-vectors

$$\begin{eqnarray} { B }_{ 1} &=& \left( { { a }_{ 1} { \vec{e} }_{ 1}} \right) \wedge { \vec{e} }_{ 2} + \left( { { b }_{ 1} { \vec{e} }_{ 2}} \right) \wedge { \vec{e} }_{ 3} + \left( { { c }_{ 1} { \vec{e} }_{ 3}} \right) \wedge { \vec{e} }_{ 1} \\ { B }_{ 2} &=& \left( { { a }_{ 2} { \vec{e} }_{ 1}} \right) \wedge { \vec{e} }_{ 2} + \left( { { b }_{ 2} { \vec{e} }_{ 2}} \right) \wedge { \vec{e} }_{ 3} + \left( { { c }_{ 2} { \vec{e} }_{ 3}} \right) \wedge { \vec{e} }_{ 1}\end{eqnarray}$$
Adding those bi-vectors of course goes like this

$$ { B }_{ 1} + { B }_{ 2} = \left( { \left( { { a }_{ 1} + { a }_{ 2}} \right) { \vec{e} }_{ 1}} \right) \wedge { \vec{e} }_{ 2} + \left( { \left( { { b }_{ 1} + { b }_{ 2}} \right) { \vec{e} }_{ 2}} \right) \wedge { \vec{e} }_{ 3} + \left( { \left( { { c }_{ 1} + { c }_{ 2}} \right) { \vec{e} }_{ 3}} \right) \wedge { \vec{e} }_{ 1}$$

A blade is a wedge product of vectors. Having a 2-blade means it's a product of two vectors.

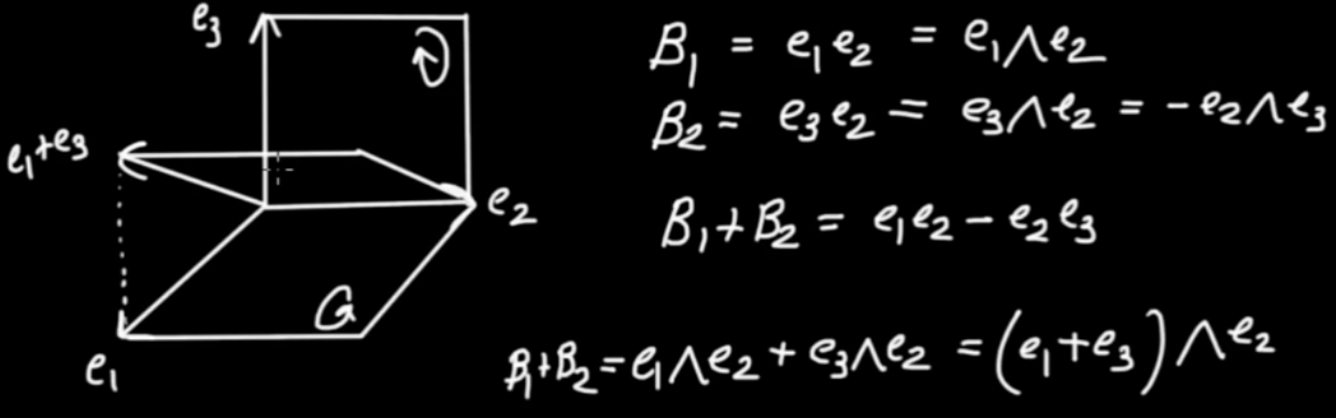Adding bi-vectors requires to find a common line. We usually do this algebraicly. Let's consider the example

$$ { B }_{ 1} = { \vec{e} }_{ 1} { \vec{e} }_{ 3}$$ $$ { B }_{ 2} = { \vec{e} }_{ 2} { \vec{e} }_{ 3}$$ $$ { B }_{ 3} = { \vec{e} }_{ 1} { \vec{e} }_{ 2}$$

We first build the sum

$$ { B }_{ 1} + { B }_{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 3} + { \vec{e} }_{ 2} { \vec{e} }_{ 3} = \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) { \vec{e} }_{ 3}$$

The common line in this addition was $ { \vec{e} }_{ 3}$. We now add to this the bi-vector $ { B }_{ 3}$.

$$ { B }_{ 1} + { B }_{ 2} + { B }_{ 3} = \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) { \vec{e} }_{ 3} + { \vec{e} }_{ 1} { \vec{e} }_{ 2}$$

Before we can do this addtion algebraicly we need to find a new common line. We need to find an alternative bi-vector for $ { \vec{e} }_{ 1} { \vec{e} }_{ 2}$ that lies in the same plane, has the same magnitude and orientation but also contains the line $ { \vec{e} }_{ 1} + { \vec{e} }_{ 2}$.

$$ { \vec{e} }_{ 1} \wedge { \vec{e} }_{ 2} = { \vec{e} }_{ 1} \wedge { \vec{e} }_{ 2} + { \vec{e} }_{ 2} \wedge { \vec{e} }_{ 2} = \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) \wedge { \vec{e} }_{ 2}$$

We then have

$$\begin{eqnarray} { B }_{ 1} + { B }_{ 2} + { B }_{ 3} &=& \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) \wedge { \vec{e} }_{ 3} + { \vec{e} }_{ 1} \wedge { \vec{e} }_{ 2} \\ { B }_{ 1} + { B }_{ 2} + { B }_{ 3} &=& \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) \wedge { \vec{e} }_{ 3} + \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) \wedge { \vec{e} }_{ 2} \\ { B }_{ 1} + { B }_{ 2} + { B }_{ 3} &=& \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) \wedge \left( { { \vec{e} }_{ 3} + { \vec{e} }_{ 2}} \right)\end{eqnarray}$$
We have sheared the bi-vector $ { \vec{e} }_{ 1} \wedge { \vec{e} }_{ 2}$ into $ \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) \wedge { \vec{e} }_{ 2}$. This allowed us to algebraicly add with $ \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right) \wedge { \vec{e} }_{ 3}$ since we had a common vector $ { \vec{e} }_{ 1} + { \vec{e} }_{ 2}$ now.

Let's reconsider a generic bi-vector.

$$\fbox{$ \displaystyle B = \left( { a { \vec{e} }_{ 1}} \right) \wedge { \vec{e} }_{ 2} + \left( { b { \vec{e} }_{ 2}} \right) \wedge { \vec{e} }_{ 3} + \left( { c { \vec{e} }_{ 3}} \right) \wedge { \vec{e} }_{ 1} $} \tag{5}$$
$$\begin{eqnarray} B &=& \left( { a { \vec{e} }_{ 1}} \right) \wedge { \vec{e} }_{ 2} - \left( { b { \vec{e} }_{ 3}} \right) \wedge { \vec{e} }_{ 2} + \left( { c { \vec{e} }_{ 3}} \right) \wedge { \vec{e} }_{ 1} \\ B &=& \left( { a { \vec{e} }_{ 1} - b { \vec{e} }_{ 3}} \right) \wedge { \vec{e} }_{ 2} - \left( { c { \vec{e} }_{ 1}} \right) \wedge { \vec{e} }_{ 3}\end{eqnarray}$$
We isolate the last term.

$$ \left( { c { \vec{e} }_{ 1}} \right) \wedge { \vec{e} }_{ 3} = \left( { \frac{ a}{ a} c { \vec{e} }_{ 1}} \right) \wedge { \vec{e} }_{ 3} = \left( { \frac{ c}{ a} a { \vec{e} }_{ 1}} \right) \wedge { \vec{e} }_{ 3} = \left( { \frac{ c}{ a} \left( { a { \vec{e} }_{ 1} - b { \vec{e} }_{ 3}} \right)} \right) \wedge { \vec{e} }_{ 3}$$

In the last step we have sheared the bi-vector without changing its magnitude and orientation since

$$ - \left( { b { \vec{e} }_{ 3}} \right) \wedge { \vec{e} }_{ 3} = 0$$

We substitute this into our expression for $ B$.
$$\begin{eqnarray} B &=& \left( { a { \vec{e} }_{ 1} - b { \vec{e} }_{ 3}} \right) \wedge { \vec{e} }_{ 2} - \left( { \frac{ c}{ a} \left( { a { \vec{e} }_{ 1} - b { \vec{e} }_{ 3}} \right)} \right) \wedge { \vec{e} }_{ 3} \\ B &=& \left( { a { \vec{e} }_{ 1} - b { \vec{e} }_{ 3}} \right) \wedge { \vec{e} }_{ 2} - \left( { a { \vec{e} }_{ 1} - b { \vec{e} }_{ 3}} \right) \wedge \left( { \frac{ c}{ a} { \vec{e} }_{ 3}} \right)\end{eqnarray}$$
$$\fbox{$ \displaystyle B = \left( { a { \vec{e} }_{ 1} - b { \vec{e} }_{ 3}} \right) \wedge \left( { { \vec{e} }_{ 2} - \frac{ c}{ a} { \vec{e} }_{ 3}} \right) $} \tag{6}$$

This proves that any bi-vector in 3D can be represented as the wedge product of two vectors and thus is a 2-blade. We do a concrete examle. Consider the addition of

$$ { B }_{ 1} = 2 { \vec{e} }_{ 1} { \vec{e} }_{ 2} - { \vec{e} }_{ 3} { \vec{e} }_{ 1}$$ $$ { B }_{ 2} = { \vec{e} }_{ 2} { \vec{e} }_{ 3}$$

This becomes

$$ { B }_{ 1} + { B }_{ 2} = 2 { \vec{e} }_{ 1} { \vec{e} }_{ 2} + { \vec{e} }_{ 2} { \vec{e} }_{ 3} - { \vec{e} }_{ 3} { \vec{e} }_{ 1}$$
By comparing this with Eq. 5 we get

$$ a = 2$$ $$ b = 1$$ $$ c = - 1$$

Substituting this into our generic solution Eq. 6 gives
$$\begin{eqnarray} B &=& \left( { a { \vec{e} }_{ 1} - b { \vec{e} }_{ 3}} \right) \wedge \left( { { \vec{e} }_{ 2} - \frac{ c}{ a} { \vec{e} }_{ 3}} \right) \\ B &=& \left( { 2 { \vec{e} }_{ 1} - { \vec{e} }_{ 3}} \right) \wedge \left( { { \vec{e} }_{ 2} + \frac{ 1}{ 2} { \vec{e} }_{ 3}} \right)\end{eqnarray}$$
Here we have again a wedge product of two vectors. Perfoming this factoriziation process allows us to find a geometric representation of the resulting 2-blade in space.

Consider the forces

$$ { \vec{F} }_{ 1} = { \vec{e} }_{ 2}$$ $$ { \vec{F} }_{ 2} = - { \vec{e} }_{ 3}$$
pulling at the end of a lever given by

$$ \vec{r} = { \vec{e} }_{ 1}$$
The resulting torque would be

$$ \tau = { \tau }_{ 1} + { \tau }_{ 2} = \vec{r} \wedge { \vec{F} }_{ 1} + \vec{r} \wedge { \vec{F} }_{ 2} = { \vec{e} }_{ 1} \wedge { \vec{e} }_{ 2} - { \vec{e} }_{ 1} \wedge { \vec{e} }_{ 3} = { \vec{e} }_{ 1} \wedge \left( { { \vec{e} }_{ 2} - { \vec{e} }_{ 3}} \right)$$

The resulting 2-blade gives us the orientation and magnitude of the torque.

Rotations and Rotors

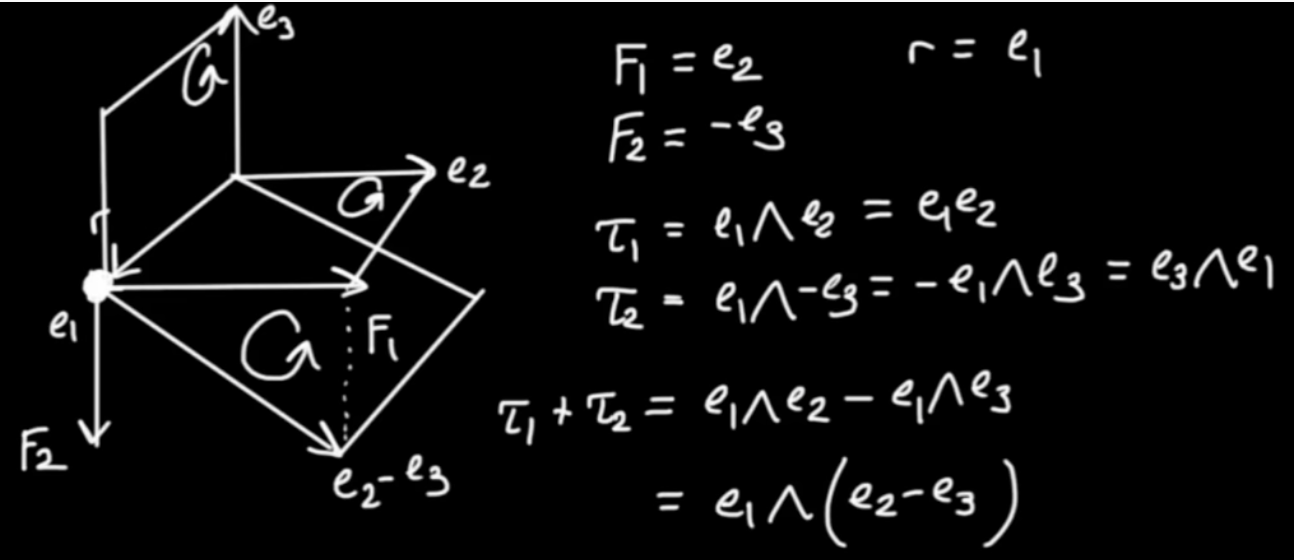$$\begin{eqnarray} \vec{u'} &=& { \vec{u} }_{ par} - { \vec{u} }_{ perp} \\ \vec{v} \vec{u'} &=& \vec{v} { \vec{u} }_{ par} - \vec{v} { \vec{u} }_{ perp} \\ \vec{v} \vec{u'} &=& { \vec{u} }_{ par} \vec{v} + { \vec{u} }_{ perp} \vec{v} \\ \vec{v} \vec{u'} &=& \left( { { \vec{u} }_{ par} + { \vec{u} }_{ perp}} \right) \vec{v} \\ \vec{v} \vec{u'} &=& \vec{u} \vec{v} \\ { \vec{v} }^{ - 1} \vec{v} \vec{u'} &=& { \vec{v} }^{ - 1} \vec{u} \vec{v}\end{eqnarray}$$
$$\fbox{$ \displaystyle \vec{u'} = { \vec{v} }^{ - 1} \vec{u} \vec{v} $} \qquad \mbox{Reflection}$$

Reflecting the result again across another vector $ \vec{w}$ gives

$$ \vec{u''} = { \vec{w} }^{ - 1} { \vec{v} }^{ - 1} \vec{u} \vec{v} \vec{w}$$

Let's use unit vectors $ { \vec{e} }_{ w} $and $ { \vec{e} }_{ v}$ instead now.

$$ \vec{u''} = { { \vec{e} }_{ w} }^{ - 1} { { \vec{e} }_{ v} }^{ - 1} \vec{u} { \vec{e} }_{ v} { \vec{e} }_{ w}$$

Due to $ { { \vec{e} }_{ w} }^{ - 1} { \vec{e} }_{ w} = 1 = { \vec{e} }_{ w} { \vec{e} }_{ w}$ we can replace this with

$$\fbox{$ \displaystyle \vec{u''} = { \vec{e} }_{ w} { \vec{e} }_{ v} \vec{u} { \vec{e} }_{ v} { \vec{e} }_{ w} $} \qquad \mbox{Rotation by twice the angle from e\_v to e\_w}$$
and due to

$$ 1 = { \vec{e} }_{ w} { \vec{e} }_{ v} { \vec{e} }_{ v} { \vec{e} }_{ w} = {\left( { \vec{e} }_{ v} { \vec{e} }_{ w} \right)}^{ - 1} \left( { { \vec{e} }_{ v} { \vec{e} }_{ w}} \right)$$
we obviously have

$$ { \vec{e} }_{ w} { \vec{e} }_{ v} = {\left( { \vec{e} }_{ v} { \vec{e} }_{ w} \right)}^{ - 1}$$

and thus
$$\fbox{$ \displaystyle \vec{u''} = {\left( { \vec{e} }_{ v} { \vec{e} }_{ w} \right)}^{ - 1} \vec{u} \left( { { \vec{e} }_{ v} { \vec{e} }_{ w}} \right) $}$$

Let's consider the problem geometrically to get an evern better idea.

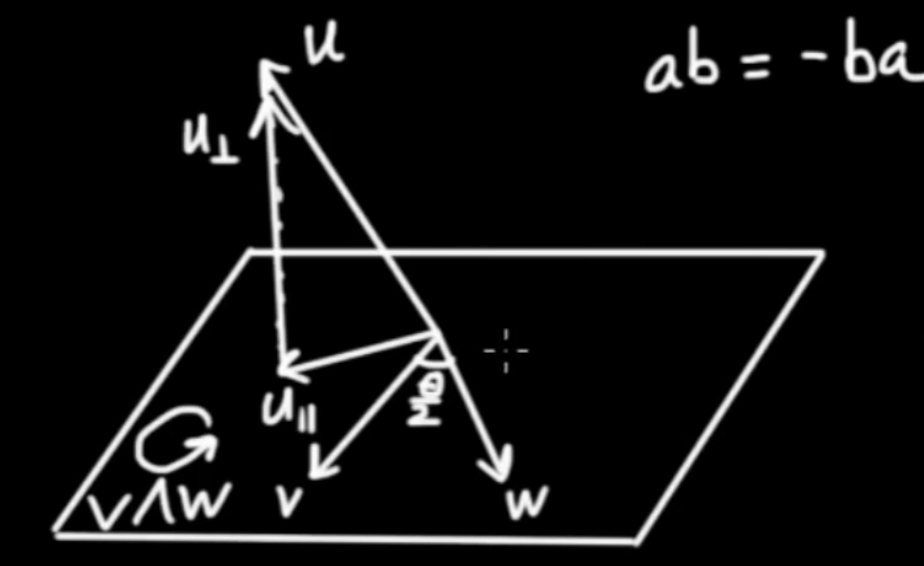We have unit vectors $ { \vec{e} }_{ v}$ and $ { \vec{e} }_{ w}$ in the plane of rotation. And our above derived rotation recipe is

$$ \vec{u''} = { \vec{e} }_{ w} { \vec{e} }_{ v} \vec{u} { \vec{e} }_{ v} { \vec{e} }_{ w} \tag{7}$$
We replace $ \vec{u}$ with $ \vec{u} = { \vec{u} }_{ par} + { \vec{u} }_{ perp}$ and get

$$\begin{eqnarray} \vec{u''} &=& { \vec{e} }_{ w} { \vec{e} }_{ v} \left( { { \vec{u} }_{ par} + { \vec{u} }_{ perp}} \right) { \vec{e} }_{ v} { \vec{e} }_{ w} \\ \vec{u''} &=& { \vec{e} }_{ w} { \vec{e} }_{ v} { \vec{u} }_{ par} { \vec{e} }_{ v} { \vec{e} }_{ w} + { \vec{e} }_{ w} { \vec{e} }_{ v} { \vec{u} }_{ perp} { \vec{e} }_{ v} { \vec{e} }_{ w}\end{eqnarray}$$Since $ { \vec{u} }_{ perp}$ is by definition perpendicular to $ { \vec{e} }_{ v}$ and $ { \vec{e} }_{ w}$ the product anti-commutes.

$$\begin{eqnarray} \vec{u''} &=& { \vec{e} }_{ w} { \vec{e} }_{ v} { \vec{u} }_{ par} { \vec{e} }_{ v} { \vec{e} }_{ w} - { \vec{e} }_{ w} { \vec{u} }_{ perp} { \vec{e} }_{ v} { \vec{e} }_{ v} { \vec{e} }_{ w} \\ \vec{u''} &=& { \vec{e} }_{ w} { \vec{e} }_{ v} { \vec{u} }_{ par} { \vec{e} }_{ v} { \vec{e} }_{ w} + { \vec{u} }_{ perp} { \vec{e} }_{ w} { \vec{e} }_{ v} { \vec{e} }_{ v} { \vec{e} }_{ w} \\ \vec{u''} &=& { \vec{e} }_{ w} { \vec{e} }_{ v} { \vec{u} }_{ par} { \vec{e} }_{ v} { \vec{e} }_{ w} + { \vec{u} }_{ perp}\end{eqnarray}$$
Obviously the double reflection through $ { \vec{e} }_{ v}$ and $ { \vec{e} }_{ w}$ does nothing to the perpendicular part or $ \vec{u}$. It's conserved. We now look at the first term. $ { \vec{u} }_{ par}$, $ { \vec{e} }_{ v}$ and $ { \vec{e} }_{ w}$ are all in the same plane. So we can reuse our knowledge or 2D rotations. The vector component $ { \vec{u} }_{ par}$ is rotated twice by the angle from $ { \vec{e} }_{ v} $to $ { \vec{e} }_{ w} $in the plane spaned by these two factors.

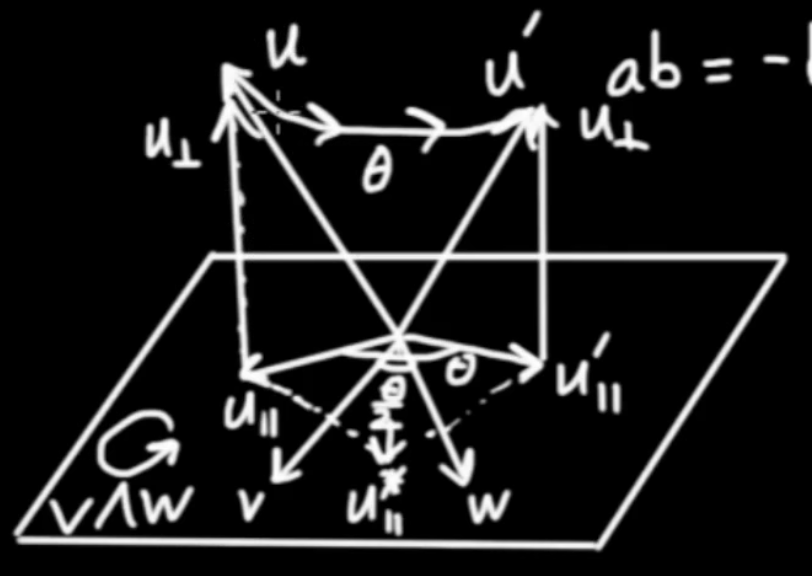Example: Let's rotate the vector $ \vec{u} = { \vec{e} }_{ 1} + { \vec{e} }_{ 3}$ in the $ { \vec{e} }_{ 1} { \vec{e} }_{ 2}$ plane by an angle $ \varphi = \pi / 2 \,$. To do that we need to construct two unit vectors in the $ { \vec{e} }_{ 1} { \vec{e} }_{ 2}$ plane separated by half of this
angle. This could be

$$ { \vec{e} }_{ v} = { \vec{e} }_{ 1}$$ $$ { \vec{e} }_{ w} = \frac{ 1}{ \sqrt{ 2}} \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right)$$

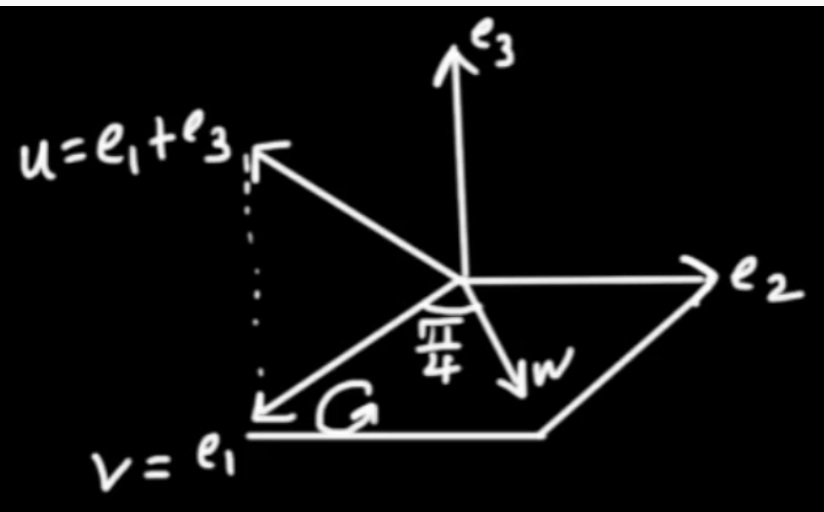The roration is then performed by Eq. 7.

$$ \vec{u''} = { \vec{e} }_{ w} { \vec{e} }_{ v} \vec{u} { \vec{e} }_{ v} { \vec{e} }_{ w}$$

$$\begin{eqnarray} { \vec{e} }_{ v} { \vec{e} }_{ w} &=& { \vec{e} }_{ v} \cdot { \vec{e} }_{ w} + { \vec{e} }_{ v} \wedge { \vec{e} }_{ w} \\ { \vec{e} }_{ v} { \vec{e} }_{ w} &=& { \vec{e} }_{ 1} \cdot \left( { \frac{ 1}{ \sqrt{ 2}} \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right)} \right) + { \vec{e} }_{ 1} \wedge \left( { \frac{ 1}{ \sqrt{ 2}} \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 2}} \right)} \right) \\ { \vec{e} }_{ v} { \vec{e} }_{ w} &=& \frac{ 1}{ \sqrt{ 2}} + \left( { \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1}} \right) \wedge { \vec{e} }_{ 2} \\ { \vec{e} }_{ v} { \vec{e} }_{ w} &=& \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} \\ { \vec{e} }_{ w} { \vec{e} }_{ v} &=& \frac{ 1}{ \sqrt{ 2}} - \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}\end{eqnarray}$$
This gives

$$\begin{eqnarray} \vec{u''} &=& { \vec{e} }_{ w} { \vec{e} }_{ v} \vec{u} { \vec{e} }_{ v} { \vec{e} }_{ w} \\ \vec{u''} &=& \left( { \frac{ 1}{ \sqrt{ 2}} - \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 3}} \right) \left( { \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \\ \vec{u''} &=& \left( { \frac{ 1}{ \sqrt{ 2}} \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 3}} \right) - \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} \left( { { \vec{e} }_{ 1} + { \vec{e} }_{ 3}} \right)} \right) \left( { \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \\ \vec{u''} &=& \left( { \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 3} - \left( { \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3}} \right)} \right) \left( { \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \\ \vec{u''} &=& \left( { \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 3} - \left( { - \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 2} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3}} \right)} \right) \left( { \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \\ \vec{u''} &=& \left( { \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 3} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 2} - \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3}} \right) \left( { \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \\ \vec{u''} &=& \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} \left( { \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 3} \left( { \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 2} \left( { \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) - \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \left( { \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \\ \vec{u''} &=& \left( { \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) + \left( { \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 3} \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 3} \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 2} \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 2} \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} - \left( { \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) \\ \vec{u''} &=& \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 3} \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 3} \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 2} \frac{ 1}{ \sqrt{ 2}} + \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 2} \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} - \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \frac{ 1}{ \sqrt{ 2}} - \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \frac{ 1}{ \sqrt{ 2}} { \vec{e} }_{ 1} { \vec{e} }_{ 2} \\ \vec{u''} &=& \frac{ 1}{ 2} { \vec{e} }_{ 1} + \frac{ 1}{ 2} { \vec{e} }_{ 2} + \frac{ 1}{ 2} { \vec{e} }_{ 3} + \frac{ 1}{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} + \frac{ 1}{ 2} { \vec{e} }_{ 2} - \frac{ 1}{ 2} { \vec{e} }_{ 1} - \frac{ 1}{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} - \frac{ 1}{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} \\ \vec{u''} &=& { \vec{e} }_{ 2} + \frac{ 1}{ 2} { \vec{e} }_{ 3} + \frac{ 1}{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} - \frac{ 1}{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} - \frac{ 1}{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} \\ \vec{u''} &=& { \vec{e} }_{ 2} + \frac{ 1}{ 2} { \vec{e} }_{ 3} + \frac{ 1}{ 2} { \vec{e} }_{ 3} \\ \vec{u''} &=& { \vec{e} }_{ 2} + { \vec{e} }_{ 3}\end{eqnarray}$$

Let the angle from $ { \vec{e} }_{ v}$ to $ { \vec{e} }_{ w}$ be $ \theta / 2 \,$. The geometric product can then be written like this

$$ { \vec{e} }_{ v} { \vec{e} }_{ w} = { \vec{e} }_{ v} \cdot { \vec{e} }_{ w} + { \vec{e} }_{ v} \wedge { \vec{e} }_{ w} = \cos \left( { \frac{ \theta }{ 2}} \right) + \sin \left( { \frac{ \theta }{ 2}} \right) I$$

with $ I = { \vec{e} }_{ 1} { \vec{e} }_{ 2}$ being orthogonal unit vectors in the plane spaned by $ { \vec{e} }_{ v}$ and $ { \vec{e} }_{ w}$. Using the Euler notation we can then write

$$ { \vec{e} }_{ v} { \vec{e} }_{ w} = { e }^{ \frac{ \theta }{ 2} I}$$ $$ I = { \vec{e} }_{ 1} { \vec{e} }_{ 2}$$

The inverse of this is obviously

$$ {\left( { \vec{e} }_{ v} { \vec{e} }_{ w} \right)}^{ - 1} = { e }^{ - \frac{ \theta }{ 2} I}$$

This gives

$$\fbox{$ \displaystyle \vec{u''} = { e }^{ - \frac{ \theta }{ 2} I} \vec{u} { e }^{ \frac{ \theta }{ 2} I} $}$$

The above expression rotates in the $ { \vec{e} }_{ 1} { \vec{e} }_{ 2}$ plane by an angle $ \theta $. The rotated vector $ \vec{u}$ doe snot have to be in the $ { \vec{e} }_{ 1} { \vec{e} }_{ 2}$ plane. The projection on the plane is rotatated. The rejection (perpendicular to the plane) is conserved.

Let's compute the length of a general bi-vector

$$\begin{eqnarray} B &=& a { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c { \vec{e} }_{ 3} { \vec{e} }_{ 1} \\ { B }^{ 2} &=& \left( { a { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) \left( { a { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) \\ { B }^{ 2} &=& a { \vec{e} }_{ 1} { \vec{e} }_{ 2} \left( { a { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) + b { \vec{e} }_{ 2} { \vec{e} }_{ 3} \left( { a { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) + c { \vec{e} }_{ 3} { \vec{e} }_{ 1} \left( { a { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) \\ { B }^{ 2} &=& \left( { a { \vec{e} }_{ 1} { \vec{e} }_{ 2} a { \vec{e} }_{ 1} { \vec{e} }_{ 2} + a { \vec{e} }_{ 1} { \vec{e} }_{ 2} b { \vec{e} }_{ 2} { \vec{e} }_{ 3} + a { \vec{e} }_{ 1} { \vec{e} }_{ 2} c { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) + \left( { b { \vec{e} }_{ 2} { \vec{e} }_{ 3} a { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b { \vec{e} }_{ 2} { \vec{e} }_{ 3} b { \vec{e} }_{ 2} { \vec{e} }_{ 3} + b { \vec{e} }_{ 2} { \vec{e} }_{ 3} c { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) + c { \vec{e} }_{ 3} { \vec{e} }_{ 1} \left( { a { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) \\ { B }^{ 2} &=& \left( { - { a }^{ 2} + a b { \vec{e} }_{ 1} { \vec{e} }_{ 3} + a c { \vec{e} }_{ 2} { \vec{e} }_{ 3}} \right) + \left( { b a { \vec{e} }_{ 3} { \vec{e} }_{ 1} - { b }^{ 2} + b c { \vec{e} }_{ 2} { \vec{e} }_{ 1}} \right) + c { \vec{e} }_{ 3} { \vec{e} }_{ 1} \left( { a { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) \\ { B }^{ 2} &=& \left( { - { a }^{ 2} + a b { \vec{e} }_{ 1} { \vec{e} }_{ 3} + a c { \vec{e} }_{ 2} { \vec{e} }_{ 3}} \right) + \left( { b a { \vec{e} }_{ 3} { \vec{e} }_{ 1} - { b }^{ 2} + b c { \vec{e} }_{ 2} { \vec{e} }_{ 1}} \right) + \left( { c { \vec{e} }_{ 3} { \vec{e} }_{ 1} a { \vec{e} }_{ 1} { \vec{e} }_{ 2} + c { \vec{e} }_{ 3} { \vec{e} }_{ 1} b { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c { \vec{e} }_{ 3} { \vec{e} }_{ 1} c { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) \\ { B }^{ 2} &=& - { a }^{ 2} + a b { \vec{e} }_{ 1} { \vec{e} }_{ 3} + a c { \vec{e} }_{ 2} { \vec{e} }_{ 3} + b a { \vec{e} }_{ 3} { \vec{e} }_{ 1} - { b }^{ 2} + b c { \vec{e} }_{ 2} { \vec{e} }_{ 1} + c a { \vec{e} }_{ 3} { \vec{e} }_{ 2} + c b { \vec{e} }_{ 1} { \vec{e} }_{ 2} - { c }^{ 2}\end{eqnarray}$$
$$\fbox{$ \displaystyle { B }^{ 2} = - { a }^{ 2} - { b }^{ 2} - { c }^{ 2} $} \tag{8}$$
Squaring a bi-vector obviously produces a negative definite scalar. We can therefore define the length of a bi-vector like this

$$\begin{eqnarray} { \left| { B} \right| }^{ 2} &=& - { B }^{ 2} \\ \left| { B} \right| &=& \sqrt{ - { B }^{ 2}}\end{eqnarray}$$
$$ \hat{B} = \frac{ B}{ \left| { B} \right|}$$

$$\fbox{$ \displaystyle { B }^{ 2} = - { \left| { B} \right| }^{ 2} $} \qquad \mbox{Bi-vector squared} \tag{9}$$

If the bi-vector has the length one we have$ \left| { B} \right| = 1$ and $ { B }^{ 2} = - 1$. The length of a bi-vector is the amount of area that is spaned by the bi-vector. Let's make up a vector.

$$ B = { \vec{e} }_{ 1} { \vec{e} }_{ 2} + { \vec{e} }_{ 2} { \vec{e} }_{ 3} - { \vec{e} }_{ 3} { \vec{e} }_{ 1}$$

Using Eq. 8 this gives

$$ { B }^{ 2} = - 3$$
$$ \left| { B} \right| = \sqrt{ - { B }^{ 2}} = \sqrt{ 3}$$

We have thus found the unit vector for $ B$ like this

$$ \hat{B} = \frac{ 1}{ \sqrt{ 3}} B$$

We now define a rotor to be an operator that rotates an object. Let's recap what we have found above.

$$ \vec{u''} = { \vec{e} }_{ w} { \vec{e} }_{ v} \vec{u} { \vec{e} }_{ v} { \vec{e} }_{ w}$$

This happens if we have the geometric product of an even number of unit vectors on both sides of the object. We therefore make the following definitions.

$$ R = { \vec{e} }_{ w} { \vec{e} }_{ v}$$ $$ { R }^{ \dag } = { \vec{e} }_{ v} { \vec{e} }_{ w}$$
with two unit vectors $ { \vec{e} }_{ w}$ and $ { \vec{e} }_{ v}$ and can then write the rotation like this

$$\fbox{$ \displaystyle \vec{u'} = R \vec{u} { R }^{ \dag } $} \qquad \mbox{Rotation of a vector}$$

We have seen above that exchanging the order of the two unit vectors rotates in the opposite direction. We can also show this as follows.

$$ R { R }^{ \dag } = { \vec{e} }_{ w} { \vec{e} }_{ v} { \vec{e} }_{ v} { \vec{e} }_{ w} = 1$$

We also have

$$\begin{eqnarray} { R }^{ \dag } &=& { \vec{e} }_{ v} { \vec{e} }_{ w} \\ { R }^{ \dag } &=& { \vec{e} }_{ v} \cdot { \vec{e} }_{ w} + { \vec{e} }_{ v} \wedge { \vec{e} }_{ w} \\ { R }^{ \dag } &=& \left| { { \vec{e} }_{ v}} \right| \left| { { \vec{e} }_{ w}} \right| \cos \left( { \frac{ \theta }{ 2}} \right) + \left| { { \vec{e} }_{ v}} \right| \left| { { \vec{e} }_{ w}} \right| \sin \left( { \frac{ \theta }{ 2}} \right) \hat{B}\end{eqnarray}$$
in which $ \hat{B}$ is the unit-bivector of the $ { \vec{e} }_{ v} { \vec{e} }_{ w}$ plane with $ { B }^{ 2} = - 1$. Since the length ofthe uni vectors is 1
this simplifies to

$$\begin{eqnarray} { R }^{ \dag } &=& \cos \left( { \frac{ \theta }{ 2}} \right) + \sin \left( { \frac{ \theta }{ 2}} \right) \hat{B} \\ { R }^{ \dag } &=& { e }^{ \frac{ \theta }{ 2} \hat{B}}\end{eqnarray}$$
and since $ R$ is the inverse of $ { R }^{ \dag }$ we also have

$$ R = { e }^{ - \frac{ \theta }{ 2} \hat{B}}$$

and thus
$$\fbox{$ \displaystyle \vec{u'} = { e }^{ - \frac{ \theta }{ 2} \hat{B}} \vec{u} { e }^{ \frac{ \theta }{ 2} \hat{B}} $} \qquad \mbox{Rotation of a vector}$$

Let's assume we have

$$ { R }_{ 1} = { \vec{e} }_{ w} { \vec{e} }_{ v}$$ $$ { { R }_{ 1} }^{ \dag } = { \vec{e} }_{ v} { \vec{e} }_{ w}$$

for a first rotation and

$$ { R }_{ 2} = { \vec{e} }_{ j} { \vec{e} }_{ i}$$ $$ { { R }_{ 2} }^{ \dag } = { \vec{e} }_{ i} { \vec{e} }_{ j}$$

for a second rotation. The combined rotation with then be

$$ \vec{u''} = { R }_{ 2} { R }_{ 1} \vec{u} { { R }_{ 1} }^{ \dag } { { R }_{ 2} }^{ \dag }$$

Since the rotors are just geometric products of unit vectors we can combine the rotors

$$ { R }_{ 3} = { R }_{ 2} { R }_{ 1} = { \vec{e} }_{ j} { \vec{e} }_{ i} { \vec{e} }_{ w} { \vec{e} }_{ v}$$

$$ { { R }_{ 3} }^{ \dag } = { { R }_{ 2} }^{ \dag } { { R }_{ 1} }^{ \dag } = { \vec{e} }_{ i} { \vec{e} }_{ j} { \vec{e} }_{ v} { \vec{e} }_{ w}$$

$$ \vec{u''} = { R }_{ 3} \vec{u} { { R }_{ 3} }^{ \dag }$$

Spinors

$$ \vec{u'} = { e }^{ - \frac{ \theta }{ 2} \hat{B}} \vec{u} { e }^{ \frac{ \theta }{ 2} \hat{B}}$$

in which $ \hat{B}$ is a unit-bivector in the plane of rotation and $ \theta $ the angle we whish to rotate the vector. What happens if we set $ \theta = 2 \pi $? This will gives us

$$\begin{eqnarray} \vec{u'} &=& R \vec{u} { R }^{ \dag } \\ \vec{u'} &=& { e }^{ - \pi \hat{B}} \vec{u} { e }^{ \pi \hat{B}} \\ \vec{u'} &=& \left( { \cos { \pi } - \hat{B} \sin { \pi } } \right) \vec{u} \left( { \cos { \pi } + \hat{B} \sin { \pi } } \right)\end{eqnarray}$$
$$ \vec{u'} = - 1 \vec{u} \left( { - 1} \right) = \vec{u}$$

As expected we end up where we have started. Let's now combine this with some arbitrary rotor $ { R }_{ 1}$. Here is our arbitrary rotation.

$$ \vec{u'} = { R }_{ 1} \vec{u} { { R }_{ 1} }^{ \dag }$$

Now we add a second rotation by $ 2 \pi $.

$$\begin{eqnarray} \vec{u''} &=& { e }^{ - \pi \hat{B}} { R }_{ 1} \vec{u} { { R }_{ 1} }^{ \dag } { e }^{ \pi \hat{B}} \\ \vec{u''} &=& \left( { { e }^{ - \pi \hat{B}} { e }^{ - \frac{ \theta }{ 2} \hat{B}}} \right) \vec{u} \left( { { e }^{ \frac{ \theta }{ 2} \hat{B}} { e }^{ \pi \hat{B}}} \right) \\ \vec{u''} &=& { e }^{ - \left( { \pi + \frac{ \theta }{ 2}} \right) \hat{B}} \vec{u} { e }^{ \left( { \pi + \frac{ \theta }{ 2}} \right) \hat{B}} \\ \vec{u''} &=& { R }_{ 2} \vec{u} { { R }_{ 2} }^{ \dag }\end{eqnarray}$$

$$\begin{eqnarray} { R }_{ 2} &=& { e }^{ - \left( { \pi + \frac{ \theta }{ 2}} \right) \hat{B}} &=& \cos \left( { \pi + \frac{ \theta }{ 2}} \right) - \sin \left( { \pi + \frac{ \theta }{ 2}} \right) \hat{B} \\ { { R }_{ 2} }^{ \dag } &=& { e }^{ \left( { \pi + \frac{ \theta }{ 2}} \right) \hat{B}} &=& \cos \left( { \pi + \frac{ \theta }{ 2}} \right) + \sin \left( { \pi + \frac{ \theta }{ 2}} \right) \hat{B}\end{eqnarray}$$
Extending our rotor with a $ 2 \pi $ rotation produces a different result. However, extending the rotor with a $ 4 \pi $ rotation brings us back to where we have been.

$$\begin{eqnarray} { R }_{ 2} &=& { e }^{ - \left( { 2 \pi } \right) \hat{B}} { R }_{ 1} &=& { e }^{ - \left( { 2 \pi + \frac{ \theta }{ 2}} \right) \hat{B}} &=& \cos \left( { 2 \pi + \frac{ \theta }{ 2}} \right) - \sin \left( { 2 \pi + \frac{ \theta }{ 2}} \right) \hat{B} &=& \cos \left( { \frac{ \theta }{ 2}} \right) - \sin \left( { \frac{ \theta }{ 2}} \right) \hat{B} &=& { R }_{ 1} \\ { { R }_{ 2} }^{ \dag } &=& { { R }_{ 1} }^{ \dag } { e }^{ \left( { 2 \pi } \right) \hat{B}} &=& { e }^{ \left( { \frac{ \theta }{ 2} + 2 \pi } \right) \hat{B}} &=& \cos \left( { 2 \pi + \frac{ \theta }{ 2}} \right) + \sin \left( { 2 \pi + \frac{ \theta }{ 2}} \right) \hat{B} &=& \cos \left( { \frac{ \theta }{ 2}} \right) + \sin \left( { \frac{ \theta }{ 2}} \right) \hat{B} &=& { { R }_{ 1} }^{ \dag }\end{eqnarray}$$
Vectors are invariant under a $ 2 \pi $ rotation. Rotors are invariant under a $ 4 \pi $ rotation and flip sign under a $ 2 \pi $ rotation. Mathematical objects that do the latter are called spinors.

Linear and spherical interpolation

$$\begin{eqnarray} \vec{v} \left( {s} \right) &=& { \vec{v} }_{ initial} + s \left( { { \vec{v} }_{ final} - { \vec{v} }_{ initial}} \right) \\ \vec{v} \left( {s} \right) &=& { \vec{v} }_{ initial} + s { \vec{v} }_{ final} - s { \vec{v} }_{ initial}\end{eqnarray}$$
$$\fbox{$ \displaystyle \vec{v} \left( {s} \right) = \left( { 1 - s} \right) { \vec{v} }_{ initial} + s { \vec{v} }_{ final} $} \qquad \mbox{Linear interpolation}$$

We do now consider two vectors $ { \vec{v} }_{ initial}$ and $ { \vec{v} }_{ final}$ both of length 1 pointing from the origin of the coordinate system to different points on the surface of a unit sphere centered at the origin of the coordinate system. The connection from the tip of the first vector to the tip of the other vector drawn on the surface of the sphere is now a so called geodesic. Let's consider the bi-vector spaned by $ { \vec{v} }_{ initial}$ and $ { \vec{v} }_{ final}$. It's intersection with the sphere will be a circle. We are now interested in interpolating from $ { \vec{v} }_{ initial}$ to $ { \vec{v} }_{ final}$ on the geodesic connecting these two points. The points of this geodesic will be elements of a specific 2D sub-space.

Our vector $ \vec{v} \left( {s} \right)$ will be a linear combination of $ { \vec{v} }_{ initial}$ and $ { \vec{v} }_{ final}$. Our job is to find the coefficients for the journey.

$$ \vec{v} \left( {s} \right) = \alpha \left( {s} \right) { \vec{v} }_{ initial} + \beta \left( {s} \right) { \vec{v} }_{ final} \tag{10}$$

The vector $ { \vec{v} }_{ final}$ is obviously a rotated version of $ { \vec{v} }_{ initial}$. In 3D the rotation of a vector is usually done like this

$$ \vec{u'} = R \vec{u} { R }^{ \dag }$$

$$ R = { e }^{ - \frac{ \theta }{ 2} \hat{B}}$$ $$ { R }^{ \dag } = { e }^{ \frac{ \theta }{ 2} \hat{B}}$$

with a a rotor $ R$ and its daggered counter part. Since we do a rotation in a 2D sub-space here (with the plane spaned by the two vectors) it will suffice to use the one-sided rotation formula

$$ { \vec{v} }_{ final} = { \vec{v} }_{ initial} R$$ with $$ R = { e }^{ \theta \hat{B}}$$

in whcih $ \hat{B}$ is the unit-bivector of the plane spaned by $ { \vec{v} }_{ final}$ and $ { \vec{v} }_{ initial}$. We can show that the rotation can like-wise be done via

$$ { \vec{v} }_{ final} = { R }^{ \dag } { \vec{v} }_{ initial}$$ with $$ { R }^{ \dag } = { e }^{ - \theta \hat{B}}$$

Let's prove this. Our proposal is

$$\begin{eqnarray} { \vec{v} }_{ initial} R &=& { R }^{ \dag } { \vec{v} }_{ initial} \\ { \vec{v} }_{ initial} { e }^{ \theta \hat{B}} &=& { e }^{ - \theta \hat{B}} { \vec{v} }_{ initial} \\ { \vec{v} }_{ initial} \left( { \cos { \theta } + \sin { \theta } \hat{B}} \right) &=& \left( { \cos { \theta } - \sin { \theta } \hat{B}} \right) { \vec{v} }_{ initial} \\ \cos { \theta } { \vec{v} }_{ initial} + \sin { \theta } { \vec{v} }_{ initial} \hat{B} &=& \cos { \theta } { \vec{v} }_{ initial} - \sin { \theta } \hat{B} { \vec{v} }_{ initial}\end{eqnarray}$$
Since $ { \vec{v} }_{ initial}$ and $ \hat{B}$ are coplanar their product anti-commutes. This gives

$$ \cos { \theta } { \vec{v} }_{ initial} + \sin { \theta } { \vec{v} }_{ initial} \hat{B} = \cos { \theta } { \vec{v} }_{ initial} + \sin { \theta } { \vec{v} }_{ initial} \hat{B}$$

q.e.d.

We now want to rotate not by $ \theta $ but by $ s \theta $ to end up at an arbitrary point on the geodesic. We therefore do

$$\begin{eqnarray} \vec{v} \left( {s} \right) &=& { \vec{v} }_{ initial} R \left( {s} \right) \\ \vec{v} \left( {s} \right) &=& { \vec{v} }_{ initial} { e }^{ s \theta \hat{B}} \\ \vec{v} \left( {s} \right) &=& { \vec{v} }_{ initial} { { e }^{ \theta \hat{B}} }^{ s}\end{eqnarray}$$
$$ \vec{v} \left( {s} \right) = { \vec{v} }_{ initial} { R }^{ s}$$ $$ R = { e }^{ \theta \hat{B}}$$

If we want to make this a left-handed oepration ew need to multiply with the dagged version of the rotor.

$$ \vec{v} \left( {s} \right) = { { R }^{ \dag } }^{ s} { \vec{v} }_{ initial}$$ $$ R = { e }^{ - \theta \hat{B}}$$

Let's look at some interesting properties of rotors. We we take the conjugate twice we of course end up at the original version.

$$\fbox{$ \displaystyle { R }^{ \dag \dag } = R $}$$

We also have

$$\fbox{$ \displaystyle {\left( { R }_{ 1} { R }_{ 2} \right)}^{ \dag } = { { R }_{ 2} }^{ \dag } { { R }_{ 1} }^{ \dag } $} \tag{11}$$
We can see this as follows. Let be $ { R }_{ 1} = { \vec{e} }_{ a} { \vec{e} }_{ b}$ and $ { R }_{ 2} = { \vec{e} }_{ c} { \vec{e} }_{ d}$. Daggering means write to product in the reverse order. This gives us

$$ {\left( { R }_{ 1} { R }_{ 2} \right)}^{ \dag } = {\left( { \vec{e} }_{ a} { \vec{e} }_{ b} { \vec{e} }_{ c} { \vec{e} }_{ d} \right)}^{ \dag } = { \vec{e} }_{ d} { \vec{e} }_{ c} { \vec{e} }_{ b} { \vec{e} }_{ a} = { { R }_{ 2} }^{ \dag } { { R }_{ 1} }^{ \dag }$$

Let's go back to our parameterisation Eq. 10 now.

$$\begin{eqnarray} \vec{v} \left( {s} \right) &=& \alpha \left( {s} \right) { \vec{v} }_{ initial} + \beta \left( {s} \right) { \vec{v} }_{ final} \\ { \vec{v} }_{ initial} { R }^{ s} &=& \alpha \left( {s} \right) { \vec{v} }_{ initial} + \beta \left( {s} \right) { \vec{v} }_{ initial} R \tag{12}\end{eqnarray}$$

We still need to determine the coefficients $ \alpha \left( {s} \right)$ and $ \beta \left( {s} \right)$. If we solve for $ \alpha \left( {s} \right)$ we still have the unknown $ \beta \left( {s} \right)$ in the way. We can get rid of it by recognizing that wedges a vector with itself return zero. We therefore wedge both sides of the equation with $ { \vec{v} }_{ initial} R$.

$$\begin{eqnarray} \left( { { \vec{v} }_{ initial} { R }^{ s}} \right) \wedge \left( { { \vec{v} }_{ initial} R} \right) &=& \left( { \alpha \left( {s} \right) { \vec{v} }_{ initial} + \beta \left( {s} \right) { \vec{v} }_{ initial} R} \right) \wedge \left( { { \vec{v} }_{ initial} R} \right) \\ \left( { { \vec{v} }_{ initial} { R }^{ s}} \right) \wedge \left( { { \vec{v} }_{ initial} R} \right) &=& \left( { \alpha \left( {s} \right) { \vec{v} }_{ initial} + \beta \left( {s} \right) { \vec{v} }_{ initial} R} \right) \wedge \left( { { \vec{v} }_{ initial} R} \right) \\ \left( { { \vec{v} }_{ initial} { R }^{ s}} \right) \wedge \left( { { \vec{v} }_{ initial} R} \right) &=& \left( { \alpha \left( {s} \right) { \vec{v} }_{ initial}} \right) \wedge \left( { { \vec{v} }_{ initial} R} \right)\end{eqnarray}$$
We now remember that we have

$$ \vec{u} \wedge \vec{v} = \frac{ 1}{ 2} \left( { \vec{u} \vec{v} - \vec{v} \vec{u}} \right) \tag{13}$$
We use this on the left side and get

$$ \frac{ 1}{ 2} \left( { { \vec{v} }_{ initial} { R }^{ s} { \vec{v} }_{ initial} R - { \vec{v} }_{ initial} R { \vec{v} }_{ initial} { R }^{ s}} \right) = \left( { \alpha \left( {s} \right) { \vec{v} }_{ initial}} \right) \wedge \left( { { \vec{v} }_{ initial} R} \right)$$
and do it on the right sire as well and get

$$\begin{eqnarray} \frac{ 1}{ 2} \left( { { \vec{v} }_{ initial} { R }^{ s} { \vec{v} }_{ initial} R - { \vec{v} }_{ initial} R { \vec{v} }_{ initial} { R }^{ s}} \right) &=& \frac{ 1}{ 2} \left( { \alpha \left( {s} \right) { \vec{v} }_{ initial} { \vec{v} }_{ initial} R - { \vec{v} }_{ initial} R \alpha \left( {s} \right) { \vec{v} }_{ initial}} \right) \\ { \vec{v} }_{ initial} { R }^{ s} { \vec{v} }_{ initial} R - { \vec{v} }_{ initial} R { \vec{v} }_{ initial} { R }^{ s} &=& \alpha \left( {s} \right) { { \vec{v} }_{ initial} }^{ 2} R - { \vec{v} }_{ initial} R \alpha \left( {s} \right) { \vec{v} }_{ initial}\end{eqnarray}$$
We have shown above that we can exchange the order of $ { \vec{v} }_{ initial} { R }^{ s}$ if we use the daggered version.

$$\begin{eqnarray} { { R }^{ s} }^{ \dag } { { \vec{v} }_{ initial} }^{ 2} R - { R }^{ \dag } { { \vec{v} }_{ initial} }^{ 2} { R }^{ s} &=& \alpha \left( {s} \right) { { \vec{v} }_{ initial} }^{ 2} R - \alpha \left( {s} \right) { R }^{ \dag } { { \vec{v} }_{ initial} }^{ 2} \\ { \left| { { \vec{v} }_{ initial}} \right| }^{ 2} { { R }^{ s} }^{ \dag } R - { \left| { { \vec{v} }_{ initial}} \right| }^{ 2} { R }^{ \dag } { R }^{ s} &=& \alpha \left( {s} \right) \left( { { \left| { { \vec{v} }_{ initial}} \right| }^{ 2} R - { \left| { { \vec{v} }_{ initial}} \right| }^{ 2} { R }^{ \dag }} \right)\end{eqnarray}$$
Since we are operating on a unit-sphere the vectors $ { \vec{v} }_{ initial}$ and $ { \vec{v} }_{ final}$ have length 1. We can therefore write

$$ { { R }^{ s} }^{ \dag } R - { R }^{ \dag } { R }^{ s} = \alpha \left( {s} \right) \left( { R - { R }^{ \dag }} \right)$$

We look at the second term $ { R }^{ \dag } { R }^{ s}$ and transform that using Eq. 11.

$$ { R }^{ \dag } { R }^{ s} = {\left( { R }^{ { s }^{ \dag }} R \right)}^{ \dag }$$
This gets us

$$ { { R }^{ s} }^{ \dag } R - {\left( { R }^{ { s }^{ \dag }} R \right)}^{ \dag } = \alpha \left( {s} \right) \left( { R - { R }^{ \dag }} \right) \tag{14}$$
On the left we have a rotor minus its conjugate now. On the right side we also have a rotor minus its conjugate. Let's expand the right side using Eulers formula.

$$\begin{eqnarray} R - { R }^{ \dag } &=& { e }^{ \theta \hat{B}} - { e }^{ - \theta \hat{B}} \\ R - { R }^{ \dag } &=& \cos { \theta } + \sin { \theta } \hat{B} - \left( { \cos { \theta } - \sin { \theta } \hat{B}} \right) \\ R - { R }^{ \dag } &=& 2 \sin { \theta } \hat{B} \tag{15}\end{eqnarray}$$We can do the same on the left side and get

$$ { { R }^{ s} }^{ \dag } R = { e }^{ - s \theta \hat{B}} { e }^{ \theta \hat{B}}$$

$$ { { R }^{ s} }^{ \dag } R = { e }^{ - s \theta \hat{B}} { e }^{ \theta \hat{B}} = { e }^{ \left( { 1 - s} \right) \theta \hat{B}}$$

We now substract the conjugate

$$\begin{eqnarray} { { R }^{ s} }^{ \dag } R - {\left( { R }^{ { s }^{ \dag }} R \right)}^{ \dag } &=& { e }^{ \left( { 1 - s} \right) \theta \hat{B}} - { e }^{ - \left( { 1 - s} \right) \theta \hat{B}} \\ { { R }^{ s} }^{ \dag } R - {\left( { R }^{ { s }^{ \dag }} R \right)}^{ \dag } &=& \cos \left( { \left( { 1 - s} \right) \theta } \right) + \sin \left( { \left( { 1 - s} \right) \theta } \right) \hat{B} - \cos \left( { \left( { 1 - s} \right) \theta } \right) - \sin \left( { \left( { 1 - s} \right) \theta } \right) \hat{B} \\ { { R }^{ s} }^{ \dag } R - {\left( { R }^{ { s }^{ \dag }} R \right)}^{ \dag } &=& 2 \sin \left( { \left( { 1 - s} \right) \theta } \right) \hat{B}\end{eqnarray}$$

Substituting this into Eq. 14 gives

$$ 2 \sin \left( { \left( { 1 - s} \right) \theta } \right) \hat{B} = 2 \alpha \left( {s} \right) \sin { \theta } \hat{B}$$

$$\fbox{$ \displaystyle \alpha \left( {s} \right) = \frac{ \sin \left( { \left( { 1 - s} \right) \theta } \right)}{ \sin { \theta } } $}$$

We reconsider Eq. 12 now and solve for $ \beta $ by wedging on the left with $ { \vec{v} }_{ initial}$ to get rid of the alpha term on the right.

$$\begin{eqnarray} { \vec{v} }_{ initial} { R }^{ s} &=& \alpha \left( {s} \right) { \vec{v} }_{ initial} + \beta \left( {s} \right) { \vec{v} }_{ initial} R \\ { \vec{v} }_{ initial} \wedge \left( { { \vec{v} }_{ initial} { R }^{ s}} \right) &=& { \vec{v} }_{ initial} \wedge \left( { \alpha \left( {s} \right) { \vec{v} }_{ initial} + \beta \left( {s} \right) { \vec{v} }_{ initial} R} \right) \\ { \vec{v} }_{ initial} \wedge \left( { { \vec{v} }_{ initial} { R }^{ s}} \right) &=& { \vec{v} }_{ initial} \wedge \left( { \beta \left( {s} \right) \left( { { \vec{v} }_{ initial} R} \right)} \right)\end{eqnarray}$$

We again replace the wedge product with the right hand-side of Eq. 13

$$\begin{eqnarray} \frac{ 1}{ 2} \left( { { \vec{v} }_{ initial} { \vec{v} }_{ initial} { R }^{ s} - { \vec{v} }_{ initial} { R }^{ s} { \vec{v} }_{ initial}} \right) &=& \frac{ 1}{ 2} \left( { { \vec{v} }_{ initial} \beta \left( {s} \right) { \vec{v} }_{ initial} R - \beta \left( {s} \right) { \vec{v} }_{ initial} R { \vec{v} }_{ initial}} \right) \\ { \left| { { \vec{v} }_{ initial}} \right| }^{ 2} { R }^{ s} - { \vec{v} }_{ initial} { R }^{ s} { \vec{v} }_{ initial} &=& \beta \left( {s} \right) { \left| { { \vec{v} }_{ initial}} \right| }^{ 2} R - \beta \left( {s} \right) { \vec{v} }_{ initial} R { \vec{v} }_{ initial} \\ { \left| { { \vec{v} }_{ initial}} \right| }^{ 2} { R }^{ s} - { \vec{v} }_{ initial} { \vec{v} }_{ initial} { { R }^{ s} }^{ \dag } &=& \beta \left( {s} \right) { \left| { { \vec{v} }_{ initial}} \right| }^{ 2} R - \beta \left( {s} \right) { \vec{v} }_{ initial} { \vec{v} }_{ initial} { R }^{ \dag } \\ { \left| { { \vec{v} }_{ initial}} \right| }^{ 2} { R }^{ s} - { \left| { { \vec{v} }_{ initial}} \right| }^{ 2} { { R }^{ s} }^{ \dag } &=& \beta \left( {s} \right) { \left| { { \vec{v} }_{ initial}} \right| }^{ 2} R - \beta \left( {s} \right) { \left| { { \vec{v} }_{ initial}} \right| }^{ 2} { R }^{ \dag } \\ { R }^{ s} - { { R }^{ s} }^{ \dag } &=& \beta \left( {s} \right) R - \beta \left( {s} \right) { R }^{ \dag } \\ { R }^{ s} - { { R }^{ s} }^{ \dag } &=& \beta \left( {s} \right) \left( { R - { R }^{ \dag }} \right)\end{eqnarray}$$
With Eq. 15 we get
$$ { R }^{ s} - { { R }^{ s} }^{ \dag } = 2 \beta \left( {s} \right) \sin { \theta } \hat{B} \tag{16}$$
We work on the left side

$$\begin{eqnarray} { R }^{ s} - { { R }^{ s} }^{ \dag } &=& { e }^{ s \theta \hat{B}} - { e }^{ - s \theta \hat{B}} \\ { R }^{ s} - { { R }^{ s} }^{ \dag } &=& \cos \left( { s \theta } \right) + \sin \left( { s \theta } \right) \hat{B} - \left( { \cos \left( { s \theta } \right) - \sin \left( { s \theta } \right) \hat{B}} \right) \\ { R }^{ s} - { { R }^{ s} }^{ \dag } &=& 2 \sin \left( { s \theta } \right) \hat{B}\end{eqnarray}$$

This substituted into Eq. 16 gives

$$\begin{eqnarray} 2 \sin \left( { s \theta } \right) \hat{B} &=& 2 \beta \left( {s} \right) \sin { \theta } \hat{B} \\ \sin \left( { s \theta } \right) \hat{B} &=& \beta \left( {s} \right) \sin { \theta } \hat{B}\end{eqnarray}$$
$$\fbox{$ \displaystyle \beta \left( {s} \right) = \frac{ \sin \left( { s \theta } \right)}{ \sin { \theta } } $}$$

Inserting the two now determined coefficients into our original construct gives us the spherical interploation.

$$\fbox{$ \displaystyle \vec{v} \left( {s} \right) = \alpha \left( {s} \right) { \vec{v} }_{ initial} + \beta \left( {s} \right) { \vec{v} }_{ final} $}$$

The angle $ \theta $ between the two 3D vectors $ { \vec{v} }_{ initial}$ and $ { \vec{v} }_{ final}$ canof cours ebe determined via

$$ { \vec{v} }_{ initial} \cdot { \vec{v} }_{ final} = \cos { \theta } $$

Quaternions

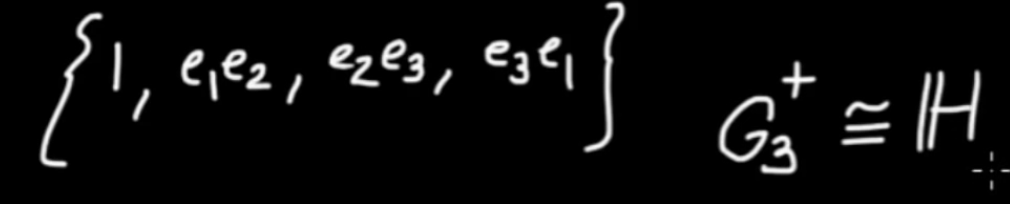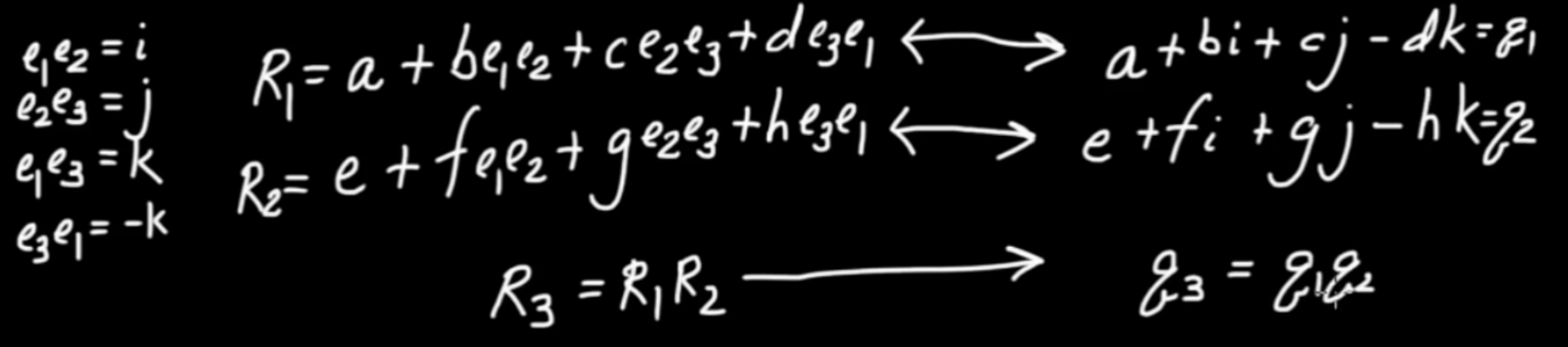$$ R = a + b { \vec{e} }_{ 1} { \vec{e} }_{ 2} + c { \vec{e} }_{ 2} { \vec{e} }_{ 3} + d { \vec{e} }_{ 3} { \vec{e} }_{ 1}$$
Rotors have the special feature

$$\fbox{$ \displaystyle { R }^{ \dag } R = R { R }^{ \dag } = 1 $} \qquad \mbox{Definition of a rotor} \tag{17}$$
Let's recap that dagger stands for swapping the order of unit-vectors. So

$$\begin{eqnarray} R &=& a + B \\ R &=& a + b { \vec{e} }_{ 1} { \vec{e} }_{ 2} + c { \vec{e} }_{ 2} { \vec{e} }_{ 3} + d { \vec{e} }_{ 3} { \vec{e} }_{ 1}\end{eqnarray}$$
$$\begin{eqnarray} { R }^{ \dag } &=& a + b { \vec{e} }_{ 2} { \vec{e} }_{ 1} + c { \vec{e} }_{ 3} { \vec{e} }_{ 2} + d { \vec{e} }_{ 1} { \vec{e} }_{ 3} \\ { R }^{ \dag } &=& a - b { \vec{e} }_{ 1} { \vec{e} }_{ 2} - c { \vec{e} }_{ 2} { \vec{e} }_{ 3} - { \vec{e} }_{ } d { \vec{e} }_{ 3} { \vec{e} }_{ 1} \\ { R }^{ \dag } &=& a - B\end{eqnarray}$$
For a rotor (magnitude = 1) this leads to the reverse operation (see Eq. 17).

$$\begin{eqnarray} { R }^{ \dag } R &=& \left( { a - B} \right) \left( { a + B} \right) \\ { R }^{ \dag } R &=& { a }^{ 2} + a B - B a - { B }^{ 2} \\ { R }^{ \dag } R &=& { a }^{ 2} - { B }^{ 2}\end{eqnarray}$$
In Rotations and Rotors there in Eq. 8 we have seen that

$$ { \left| { B} \right| }^{ 2} = - { B }^{ 2}$$

We can therefore write

$$\begin{eqnarray} { R }^{ \dag } R &=& { a }^{ 2} + { \left| { B} \right| }^{ 2} \\ { R }^{ \dag } R &=& { a }^{ 2} + { b }^{ 2} + { c }^{ 2} + { d }^{ 2}\end{eqnarray}$$
and together with Eq. 17 say that the set of rotors in 3D is the sub-set of 3D for which the condition

$$\fbox{$ \displaystyle { a }^{ 2} + { b }^{ 2} + { c }^{ 2} + { d }^{ 2} = 1 $} \qquad \mbox{Condition of a rotor} \tag{18}$$
is fulfilled. This is the same thing as saying that every rotor has magnitude 1 and thus is a unit-quaternion. A unit quaternion just rotates (does nothing else). If others talk about quaternions we now know that they actually talk about the sub-space of R3 with only even grades. If others talk about unit-quaternions we know they talk about rotors. If we multiply two unit-quaternions (rotors) we get another unit-quaternion (rotor). Let's prove that this is true.

$$\begin{eqnarray} { R }_{ 1} &=& a + b { \vec{e} }_{ 1} { \vec{e} }_{ 2} + c { \vec{e} }_{ 2} { \vec{e} }_{ 3} + d { \vec{e} }_{ 3} { \vec{e} }_{ 1} \\ { R }_{ 2} &=& e + f { \vec{e} }_{ 1} { \vec{e} }_{ 2} + g { \vec{e} }_{ 2} { \vec{e} }_{ 3} + h { \vec{e} }_{ 3} { \vec{e} }_{ 1}\end{eqnarray}$$

$$ { R }_{ 1} { R }_{ 2} = \left( { a + b { \vec{e} }_{ 1} { \vec{e} }_{ 2} + c { \vec{e} }_{ 2} { \vec{e} }_{ 3} + d { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) \left( { e + f { \vec{e} }_{ 1} { \vec{e} }_{ 2} + g { \vec{e} }_{ 2} { \vec{e} }_{ 3} + h { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right)$$

$$\begin{eqnarray} { R }_{ 1} { R }_{ 2} &=& a \left( { e + f { \vec{e} }_{ 1} { \vec{e} }_{ 2} + g { \vec{e} }_{ 2} { \vec{e} }_{ 3} + h { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) + b { \vec{e} }_{ 1} { \vec{e} }_{ 2} \left( { e + f { \vec{e} }_{ 1} { \vec{e} }_{ 2} + g { \vec{e} }_{ 2} { \vec{e} }_{ 3} + h { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) + c { \vec{e} }_{ 2} { \vec{e} }_{ 3} \left( { e + f { \vec{e} }_{ 1} { \vec{e} }_{ 2} + g { \vec{e} }_{ 2} { \vec{e} }_{ 3} + h { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) + d { \vec{e} }_{ 3} { \vec{e} }_{ 1} \left( { e + f { \vec{e} }_{ 1} { \vec{e} }_{ 2} + g { \vec{e} }_{ 2} { \vec{e} }_{ 3} + h { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) \\ { R }_{ 1} { R }_{ 2} &=& \left( { a e + a f { \vec{e} }_{ 1} { \vec{e} }_{ 2} + g { \vec{e} }_{ 2} { \vec{e} }_{ 3} + h { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) + \left( { b e { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b { \vec{e} }_{ 1} { \vec{e} }_{ 2} f { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b { \vec{e} }_{ 1} { \vec{e} }_{ 2} g { \vec{e} }_{ 2} { \vec{e} }_{ 3} + b { \vec{e} }_{ 1} { \vec{e} }_{ 2} h { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) + \left( { e c { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c { \vec{e} }_{ 2} { \vec{e} }_{ 3} f { \vec{e} }_{ 1} { \vec{e} }_{ 2} + c { \vec{e} }_{ 2} { \vec{e} }_{ 3} g { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c { \vec{e} }_{ 2} { \vec{e} }_{ 3} h { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) + \left( { e d { \vec{e} }_{ 3} { \vec{e} }_{ 1} + d { \vec{e} }_{ 3} { \vec{e} }_{ 1} f { \vec{e} }_{ 1} { \vec{e} }_{ 2} + g d { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + h d { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) \\ { R }_{ 1} { R }_{ 2} &=& \left( { a e + a f { \vec{e} }_{ 1} { \vec{e} }_{ 2} + g { \vec{e} }_{ 2} { \vec{e} }_{ 3} + h { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) + \left( { b e { \vec{e} }_{ 1} { \vec{e} }_{ 2} - b f + b g { \vec{e} }_{ 1} { \vec{e} }_{ 3} + b h { \vec{e} }_{ 2} { \vec{e} }_{ 3}} \right) + \left( { e c { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c f { \vec{e} }_{ 3} { \vec{e} }_{ 1} - c g + c h { \vec{e} }_{ 2} { \vec{e} }_{ 1}} \right) + \left( { e d { \vec{e} }_{ 3} { \vec{e} }_{ 1} + d f { \vec{e} }_{ 3} { \vec{e} }_{ 2} + g d { \vec{e} }_{ 1} { \vec{e} }_{ 2} - h d} \right) \\ { R }_{ 1} { R }_{ 2} &=& a e + a f { \vec{e} }_{ 1} { \vec{e} }_{ 2} + a g { \vec{e} }_{ 2} { \vec{e} }_{ 3} + a h { \vec{e} }_{ 3} { \vec{e} }_{ 1} + b e { \vec{e} }_{ 1} { \vec{e} }_{ 2} - b f + b g { \vec{e} }_{ 1} { \vec{e} }_{ 3} + b h { \vec{e} }_{ 2} { \vec{e} }_{ 3} + e c { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c f { \vec{e} }_{ 3} { \vec{e} }_{ 1} - c g + c h { \vec{e} }_{ 2} { \vec{e} }_{ 1} + e d { \vec{e} }_{ 3} { \vec{e} }_{ 1} + d f { \vec{e} }_{ 3} { \vec{e} }_{ 2} + g d { \vec{e} }_{ 1} { \vec{e} }_{ 2} - h d\end{eqnarray}$$
$$\fbox{$ \displaystyle { R }_{ 1} { R }_{ 2} = a e - b f - c g - h d + \left( { a f + b e + g d - c h} \right) { \vec{e} }_{ 1} { \vec{e} }_{ 2} + \left( { a g + b h + e c - d f} \right) { \vec{e} }_{ 2} { \vec{e} }_{ 3} + \left( { a h + c f + e d - b g} \right) { \vec{e} }_{ 3} { \vec{e} }_{ 1} $}$$

This expression is neat to know in case we need to actually calculate the product of rotors (corresponds to a matrix multiplication in linear algebra). But we still need to prove that the result of such a multiplication is still a unit-quaternion (rotor). A rotor is always the product of two vectors. Let's say

$$ { R }_{ 1} = \vec{u} \vec{v}$$ $$ { R }_{ 2} = \vec{w} \vec{x}$$

We then have

$$ { R }_{ 1} { R }_{ 2} = \vec{u} \vec{v} \vec{w} \vec{x}$$ $$ {\left( { R }_{ 1} { R }_{ 2} \right)}^{ \dag } = \vec{x} \vec{w} \vec{v} \vec{u} = { { R }_{ 2} }^{ \dag } { { R }_{ 1} }^{ \dag }$$

The definition of a rotor was $ { R }^{ \dag } R = 1$. Let' see.

$$ {\left( { R }_{ 1} { R }_{ 2} \right)}^{ \dag } \left( { { R }_{ 1} { R }_{ 2}} \right) = { { R }_{ 2} }^{ \dag } { { R }_{ 1} }^{ \dag } { R }_{ 1} { R }_{ 2} = { { R }_{ 2} }^{ \dag } { R }_{ 2} = 1$$

This proves that the product of two rotors is also a rotor. If it is a rotor the condition Eq. 18 applies. This means we also have

$$ \left| { { R }_{ 1} { R }_{ 2}} \right| = 1$$

The rotors therefore form a group. They close. They inherit associativity from R3. They have an inverse whch is the dagger.

Duality and the Cross Product

Pseudo-scalar in two dimensions

$$ { I }^{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} = - { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 2} { \vec{e} }_{ 1} = - 1$$

$$ { I }^{ - 1} I = { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} = 1$$

Products with $ I$:

$$ I { \vec{e} }_{ 1} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} = - { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} = - { \vec{e} }_{ 1} I$$

$$ I { \vec{e} }_{ 1} { \vec{e} }_{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} = { \vec{e} }_{ 1} I$$

Pseudo-scalar in three dimensions

$$ { I }^{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 3} = - 1$$

$$ { I }^{ - 1} I = { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} = 1$$
Products with $ I$:

$$ I { \vec{e} }_{ 1} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} = { \vec{e} }_{ 1} I$$

$$ I { \vec{e} }_{ 1} { \vec{e} }_{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} I$$

$$ I { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} I$$

Pseudo-scalar in four dimensions

$$ { I }^{ - 1} I = { \vec{e} }_{ 4} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} = 1$$

Products with $ I$:

$$ I { \vec{e} }_{ 1} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} { \vec{e} }_{ 1} = { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} = { \vec{e} }_{ 1} I$$

$$ I { \vec{e} }_{ 1} { \vec{e} }_{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} { \vec{e} }_{ 1} { \vec{e} }_{ 2} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} I$$

$$ I { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} = - { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} = - { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} I$$

$$ I { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} = { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 4} I$$

Duality in three dimensions

$$\begin{eqnarray} { \vec{e} }_{ 1} I &=& { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} &=& { \vec{e} }_{ 2} { \vec{e} }_{ 3} \\ { \vec{e} }_{ 2} I &=& { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} &=& { \vec{e} }_{ 3} { \vec{e} }_{ 1} \\ { \vec{e} }_{ 3} I &=& { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} &=& { \vec{e} }_{ 1} { \vec{e} }_{ 2}\end{eqnarray}$$

And for bi-vectors:

$$\begin{eqnarray} { \vec{e} }_{ 1} { \vec{e} }_{ 2} I &=& { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} &=& - { \vec{e} }_{ 3} \\ { \vec{e} }_{ 2} { \vec{e} }_{ 3} I &=& { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} &=& - { \vec{e} }_{ 1} \\ { \vec{e} }_{ 3} { \vec{e} }_{ 1} I &=& { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} &=& - { \vec{e} }_{ 2}\end{eqnarray}$$
Let's consider a general bi-vector in $ { R }^{ 3}$ and make use of the above findings.

$$\begin{eqnarray} B &=& { B }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} + { B }_{ 2} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + { B }_{ 3} { \vec{e} }_{ 3} { \vec{e} }_{ 1} \\ B &=& { B }_{ 1} { \vec{e} }_{ 3} I - { B }_{ 2} { \vec{e} }_{ 1} I - { B }_{ 3} { \vec{e} }_{ 2} I \\ B &=& \left( { { B }_{ 1} { \vec{e} }_{ 3} + { B }_{ 2} { \vec{e} }_{ 1} + { B }_{ 3} { \vec{e} }_{ 2}} \right) I \\ B &=& \left( { { B }_{ 2} { \vec{e} }_{ 1} + { B }_{ 3} { \vec{e} }_{ 2} + { B }_{ 1} { \vec{e} }_{ 3}} \right) I \\ B &=& \left( { { b }_{ 1} { \vec{e} }_{ 1} + { b }_{ 2} { \vec{e} }_{ 2} + { b }_{ 3} { \vec{e} }_{ 3}} \right) I\end{eqnarray}$$
$$\fbox{$ \displaystyle B = \vec{b} I $} \qquad \mbox{Bi-vector Representation}$$

We can transform a vector $ \vec{b} = \left( \begin{array}{ccc}
{ b }_{ 1} & { b }_{ 2} & { b }_{ 3}\\
\end{array}\right)$ into a bi-vector $ B = { B }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} + { B }_{ 2} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + { B }_{ 3} { \vec{e} }_{ 3} { \vec{e} }_{ 1}$ by multiplying with $ I$ and setting $ { b }_{ 1} = { B }_{ 2}$, $ { b }_{ 2} = { B }_{ 3}$ and $ { b }_{ 3} = { B }_{ 1}$.

Let's consider a general vector in $ { R }^{ 3}$ and make use of the above findings.

$$\begin{eqnarray} \vec{b} &=& { b }_{ 1} { \vec{e} }_{ 1} + { b }_{ 2} { \vec{e} }_{ 2} + { b }_{ 3} { \vec{e} }_{ 3} \\ \vec{b} &=& - { b }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} I - { b }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} I - { b }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} I \\ \vec{b} &=& - \left( { { b }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + { b }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1} + { b }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2}} \right) I \\ \vec{b} &=& - \left( { { b }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} + { b }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + { b }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) I \\ \vec{b} &=& - \left( { { B }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} + { B }_{ 2} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + { B }_{ 3} { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) I\end{eqnarray}$$
$$\fbox{$ \displaystyle \vec{b} = - B I $} \qquad \mbox{Vector Representation}$$

We can transform a bi-vector $ B = { B }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} + { B }_{ 2} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + { B }_{ 3} { \vec{e} }_{ 3} { \vec{e} }_{ 1}$ into a vector $ \vec{b} = \left( \begin{array}{ccc}
{ b }_{ 1} & { b }_{ 2} & { b }_{ 3}\\
\end{array}\right)$ by multiplying with $ - I$ and setting $ { b }_{ 1} = { B }_{ 2}$, $ { b }_{ 2} = { B }_{ 3}$ and $ { b }_{ 3} = { B }_{ 1}$.

$$\begin{eqnarray} { I }^{ - 1} I &=& { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} &=& 1 \\ I { I }^{ - 1} &=& { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} &=& 1\end{eqnarray}$$
By multiplying both sides of the first equation with $ { I }^{ - 1} = { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1}$ we get

$$ B { I }^{ - 1} = \vec{b} I { I }^{ - 1}$$

$$\fbox{$ \displaystyle \vec{b} = B { I }^{ - 1} $}$$

By multiplying both sides of the second equation with $ { I }^{ - 1} = { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1}$ we get

$$ \vec{b} { I }^{ - 1} = - B I { I }^{ - 1}$$

$$\fbox{$ \displaystyle B = - \vec{b} { I }^{ - 1} $}$$

We try out these equations by doing a loop. We start with $ \vec{b} = \left( \begin{array}{ccc}
{ b }_{ 1} & { b }_{ 2} & { b }_{ 3}\\
\end{array}\right)$ and build the dual.

$$ B = { \vec{b} }^{ *} = \vec{b} I$$
This gets us

$$\begin{eqnarray} B &=& \left( { { b }_{ 1} { \vec{e} }_{ 1} + { b }_{ 2} { \vec{e} }_{ 2} + { b }_{ 3} { \vec{e} }_{ 3}} \right) { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \\ B &=& { b }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + { b }_{ 2} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + { b }_{ 3} { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \\ B &=& { b }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} - { b }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 3} + { b }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} \\ B &=& { b }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} + { b }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + { b }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1}\end{eqnarray}$$

We build the dual of this to get back where we came from. Building the dual of a bi-vector is by multiplying withthe inverse pseudo-scalar.

$$\begin{eqnarray} { B }^{ *} &=& \left( { { b }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} + { b }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + { b }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) { I }^{ - 1} \\ { B }^{ *} &=& \left( { { b }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 2} + { b }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} + { b }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 1}} \right) { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} \\ { B }^{ *} &=& { b }_{ 3} { \vec{e} }_{ 3} + { b }_{ 1} { \vec{e} }_{ 1} + { b }_{ 2} { \vec{e} }_{ 2} \\ { B }^{ *} &=& \vec{b}\end{eqnarray}$$
So creating the dual twice following the above rules gets us back to where we came from.

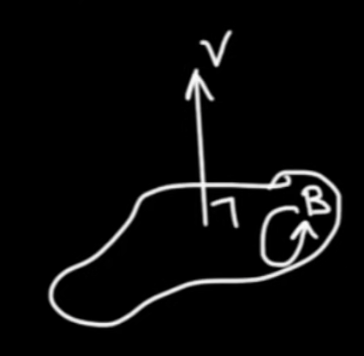$$ B = 2 { \vec{e} }_{ 1} { \vec{e} }_{ 2}$$

$$\begin{eqnarray} \vec{b} &=& B I \\ \vec{b} &=& 2 { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} \\ \vec{b} &=& 2 { \vec{e} }_{ 3}\end{eqnarray}$$
Let's consider another example.

$$ B = { \vec{e} }_{ 1} { \vec{e} }_{ 2} + { \vec{e} }_{ 2} { \vec{e} }_{ 3}$$

This gives

$$\begin{eqnarray} \vec{b} &=& B { I }^{ - 1} \\ \vec{b} &=& \left( { { \vec{e} }_{ 1} { \vec{e} }_{ 2} + { \vec{e} }_{ 2} { \vec{e} }_{ 3}} \right) \left( { { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1}} \right) \\ \vec{b} &=& { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} + { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} \\ \vec{b} &=& { \vec{e} }_{ 3} + { \vec{e} }_{ 1}\end{eqnarray}$$
This vector $ \vec{b}$ is the dual to $ B$.

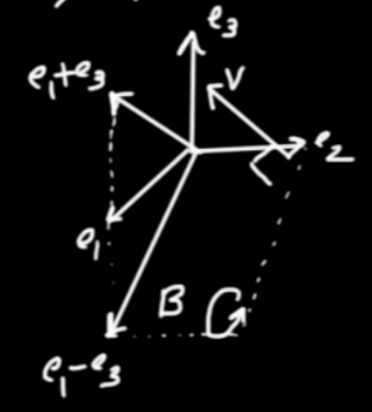$$ { B }^{ 2} = - { \left| { B} \right| }^{ 2}$$
while looking at the bi-vector representation with its dual again.

$$\begin{eqnarray} B &=& \vec{v} I \\ { B }^{ 2} &=& \vec{v} I \vec{v} I \\ { B }^{ 2} &=& \vec{v} { I }^{ 2} \vec{v} \\ { B }^{ 2} &=& - { \left| { \vec{v}} \right| }^{ 2} \\ - { \left| { B} \right| }^{ 2} &=& - { \left| { \vec{v}} \right| }^{ 2}\end{eqnarray}$$
$$\fbox{$ \displaystyle \left| { B} \right| = \left| { \vec{v}} \right| $}$$

That's interesting. The magnitude of a bi-vector is equal to the length of the corresponding dual vector. Let's consider two vectors $ \vec{a}$ and $ \vec{b}$ spaning some parallelogram.

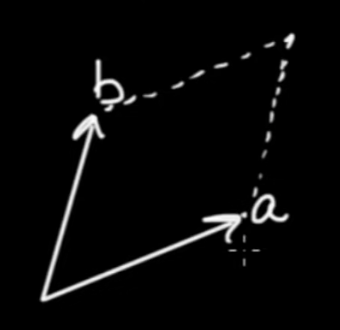$$ \vec{a} = a { \vec{e} }_{ 1} + b { \vec{e} }_{ 2} + c { \vec{e} }_{ 3}$$ $$ \vec{b} = d { \vec{e} }_{ 1} + e { \vec{e} }_{ 2} + f { \vec{e} }_{ 3}$$

$$\begin{eqnarray} \vec{v} &=& B { I }^{ - 1} \\ \vec{v} &=& \left( { \vec{a} \wedge \vec{b}} \right) { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} \\ \vec{v} &=& \frac{ 1}{ 2} \left( { \vec{a} \vec{b} - \vec{b} \vec{a}} \right) { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} \\ \vec{v} &=& \frac{ 1}{ 2} \left( { \left( { a { \vec{e} }_{ 1} + b { \vec{e} }_{ 2} + c { \vec{e} }_{ 3}} \right) \left( { d { \vec{e} }_{ 1} + e { \vec{e} }_{ 2} + f { \vec{e} }_{ 3}} \right) - \left( { d { \vec{e} }_{ 1} + e { \vec{e} }_{ 2} + f { \vec{e} }_{ 3}} \right) \left( { a { \vec{e} }_{ 1} + b { \vec{e} }_{ 2} + c { \vec{e} }_{ 3}} \right)} \right) { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} \\ \vec{v} &=& \frac{ 1}{ 2} \left( { a { \vec{e} }_{ 1} \left( { d { \vec{e} }_{ 1} + e { \vec{e} }_{ 2} + f { \vec{e} }_{ 3}} \right) + b { \vec{e} }_{ 2} \left( { d { \vec{e} }_{ 1} + e { \vec{e} }_{ 2} + f { \vec{e} }_{ 3}} \right) + c { \vec{e} }_{ 3} \left( { d { \vec{e} }_{ 1} + e { \vec{e} }_{ 2} + f { \vec{e} }_{ 3}} \right) - \left( { d { \vec{e} }_{ 1} \left( { a { \vec{e} }_{ 1} + b { \vec{e} }_{ 2} + c { \vec{e} }_{ 3}} \right) + e { \vec{e} }_{ 2} \left( { a { \vec{e} }_{ 1} + b { \vec{e} }_{ 2} + c { \vec{e} }_{ 3}} \right) + f { \vec{e} }_{ 3} \left( { a { \vec{e} }_{ 1} + b { \vec{e} }_{ 2} + c { \vec{e} }_{ 3}} \right)} \right)} \right) { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} \\ \vec{v} &=& \frac{ 1}{ 2} \left( { a d + a e { \vec{e} }_{ 1} { \vec{e} }_{ 2} + a f { \vec{e} }_{ 1} { \vec{e} }_{ 3} + b d { \vec{e} }_{ 2} { \vec{e} }_{ 1} + b e + b f { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c d { \vec{e} }_{ 3} { \vec{e} }_{ 1} + c e { \vec{e} }_{ 3} { \vec{e} }_{ 2} + c f - d a - d b { \vec{e} }_{ 1} { \vec{e} }_{ 2} - d c { \vec{e} }_{ 1} { \vec{e} }_{ 3} - e a { \vec{e} }_{ 2} { \vec{e} }_{ 1} - e b - e c { \vec{e} }_{ 2} { \vec{e} }_{ 3} - f a { \vec{e} }_{ 3} { \vec{e} }_{ 1} - f b { \vec{e} }_{ 3} { \vec{e} }_{ 2} - f c} \right) { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} \\ \vec{v} &=& \frac{ 1}{ 2} \left( { a d + b e + c f - d a - e b - f c + a e { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b d { \vec{e} }_{ 2} { \vec{e} }_{ 1} - d b { \vec{e} }_{ 1} { \vec{e} }_{ 2} - e a { \vec{e} }_{ 2} { \vec{e} }_{ 1} + a f { \vec{e} }_{ 1} { \vec{e} }_{ 3} + c d { \vec{e} }_{ 3} { \vec{e} }_{ 1} - d c { \vec{e} }_{ 1} { \vec{e} }_{ 3} - f a { \vec{e} }_{ 3} { \vec{e} }_{ 1} + b f { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c e { \vec{e} }_{ 3} { \vec{e} }_{ 2} - e c { \vec{e} }_{ 2} { \vec{e} }_{ 3} - f b { \vec{e} }_{ 3} { \vec{e} }_{ 2}} \right) { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} \\ \vec{v} &=& \frac{ 1}{ 2} \left( { a e { \vec{e} }_{ 1} { \vec{e} }_{ 2} + b d { \vec{e} }_{ 2} { \vec{e} }_{ 1} - d b { \vec{e} }_{ 1} { \vec{e} }_{ 2} - e a { \vec{e} }_{ 2} { \vec{e} }_{ 1} + a f { \vec{e} }_{ 1} { \vec{e} }_{ 3} + c d { \vec{e} }_{ 3} { \vec{e} }_{ 1} - d c { \vec{e} }_{ 1} { \vec{e} }_{ 3} - f a { \vec{e} }_{ 3} { \vec{e} }_{ 1} + b f { \vec{e} }_{ 2} { \vec{e} }_{ 3} + c e { \vec{e} }_{ 3} { \vec{e} }_{ 2} - e c { \vec{e} }_{ 2} { \vec{e} }_{ 3} - f b { \vec{e} }_{ 3} { \vec{e} }_{ 2}} \right) { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} \\ \vec{v} &=& \frac{ 1}{ 2} \left( { a e { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} + b d { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} - d b { \vec{e} }_{ 1} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} - e a { \vec{e} }_{ 2} { \vec{e} }_{ 1} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} + a f { \vec{e} }_{ 1} { \vec{e} }_{ 3} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} + c d { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1}} \right) \\ \frac{ 1}{ 2} \left( { - d c { \vec{e} }_{ 1} { \vec{e} }_{ 3} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} - f a { \vec{e} }_{ 3} { \vec{e} }_{ 1} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} + b f { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} + c e { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} - e c { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1} - f b { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 3} { \vec{e} }_{ 2} { \vec{e} }_{ 1}} \right)\end{eqnarray}$$
$$\begin{eqnarray} \vec{v} &=& \frac{ 1}{ 2} \left( { a e { \vec{e} }_{ 3} - b d { \vec{e} }_{ 3} - d b { \vec{e} }_{ 3} + e a { \vec{e} }_{ 3} - a f { \vec{e} }_{ 2} + c d { \vec{e} }_{ 2} + d c { \vec{e} }_{ 2} - f a { \vec{e} }_{ 2} + b f { \vec{e} }_{ 1} - c e { \vec{e} }_{ 1} - e c { \vec{e} }_{ 1} + f b { \vec{e} }_{ 1}} \right) \\ \vec{v} &=& \frac{ 1}{ 2} \left( { 2 a e { \vec{e} }_{ 3} - 2 b d { \vec{e} }_{ 3} - 2 a f { \vec{e} }_{ 2} + 2 c d { \vec{e} }_{ 2} + 2 b f { \vec{e} }_{ 1} - 2 c e { \vec{e} }_{ 1}} \right) \\ \vec{v} &=& a e { \vec{e} }_{ 3} - b d { \vec{e} }_{ 3} - a f { \vec{e} }_{ 2} + c d { \vec{e} }_{ 2} + b f { \vec{e} }_{ 1} - c e { \vec{e} }_{ 1} \\ \vec{v} &=& \left( { a e - b d} \right) { \vec{e} }_{ 3} - \left( { a f - c d} \right) { \vec{e} }_{ 2} + \left( { b f - c e} \right) { \vec{e} }_{ 1} \\ \vec{v} &=& \left( { b f - c e} \right) { \vec{e} }_{ 1} - \left( { a f - c d} \right) { \vec{e} }_{ 2} + \left( { a e - b d} \right) { \vec{e} }_{ 3}\end{eqnarray}$$
This leaves us with the well known formula for the cross product
$$ \vec{v} = \det \left( { \left| { \begin{array}{ccc}
{ \vec{e} }_{ 1} & - { \vec{e} }_{ 2} & { \vec{e} }_{ 3}\\ a & b & c\\ d & e & f\\
\end{array}} \right|} \right)$$

and allows us to define the cross product like this

$$\fbox{$ \displaystyle \vec{a} \times \vec{b} = \left( { \vec{a} \wedge \vec{b}} \right) { I }^{ - 1} $} \qquad \mbox{Cross Product}$$

$$\fbox{$ \displaystyle \vec{a} \wedge \vec{b} = \left( { \vec{a} \times \vec{b}} \right) I $} \qquad \mbox{Wedge Product}$$

Using this definition we can easily show a couple of attributes of the cross product.

$$ \vec{u} \times \left( { \lambda \vec{u}} \right) = \lambda \left( { \vec{u} \wedge \vec{u}} \right) { I }^{ - 1} = 0$$

$$ \vec{a} \times \vec{b} = \left( { \vec{a} \wedge \vec{b}} \right) { I }^{ - 1} = - \left( { \vec{b} \wedge \vec{a}} \right) { I }^{ - 1} = - \vec{b} \times \vec{a}$$

We have discussed addition of bi-vectors in Addition of bi-vectors and saw that this could get rather complex since we need to find a common line first. Since we can represent any bi-vector by the product of a vector with the pseudo-scalar

$$ B = \vec{v} I$$
we can simplify this a lot now.

$$\fbox{$ \displaystyle { B }_{ 1} + { B }_{ 2} = \left( { { \vec{v} }_{ 1} + { \vec{v} }_{ 2}} \right) I $}$$

with

$$ { \vec{v} }_{ 1} = { B }_{ 1} { I }^{ - 1}$$ $$ { \vec{v} }_{ 2} = { B }_{ 2} { I }^{ - 1}$$

Adding vectors is a trivial task. Mutliplying with a pseudo-scalar is as well. Neat!

With duality in mind let's reconsider rotations now. We have seen in Rotations and Rotors that a rotation is done by

$$ \vec{u''} = {\left( { \vec{e} }_{ v} { \vec{e} }_{ w} \right)}^{ - 1} \vec{u} \left( { { \vec{e} }_{ v} { \vec{e} }_{ w}} \right)$$

or

$$ \vec{u''} = { e }^{ - \frac{ \theta }{ 2} \hat{B}} \vec{u} { e }^{ \frac{ \theta }{ 2} \hat{B}}$$ $$ \hat{B} = { \vec{e} }_{ 1} { \vec{e} }_{ 2}$$

Using duality we can replace the unit bi-vector of the plane of rotation with $ \hat{B} = \hat{n} I$.

$$ \vec{u''} = { e }^{ - \frac{ \theta }{ 2} \hat{n} I} \vec{u} { e }^{ \frac{ \theta }{ 2} \hat{n} I}$$

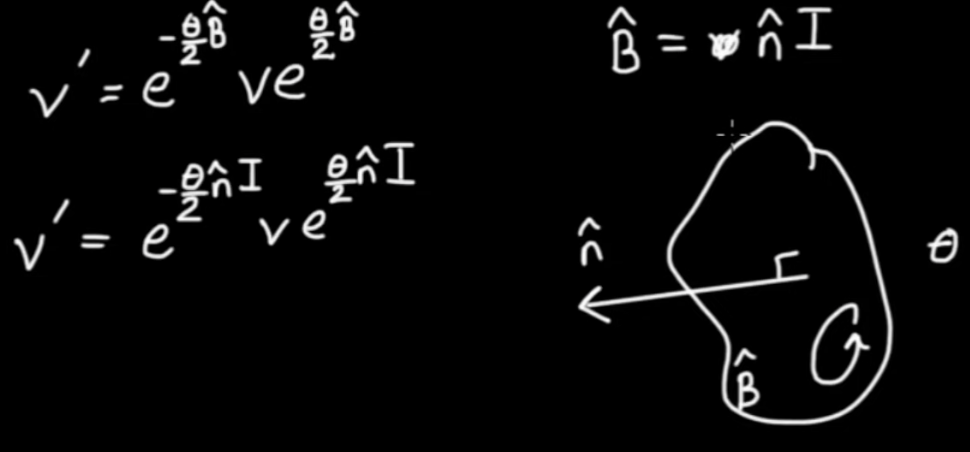Thinking of rotations around an axis is only appropriate in 3D. Thinking of rotations in a plane is appropriate in all dimensions.

Lez's consider some vector $ \vec{u}$ and a bi-vector $ B .$

$$ \vec{u} B = \vec{u} \cdot B + \vec{u} \wedge B$$

in which the scalar product was defined as the grade-1 part of the product and the wedge product as the grade-3 part of the product.

$$ \langle B \vec{c}\rangle_{ 1} = - \langle \vec{c} B\rangle_{ 1}$$ $$\fbox{$ \displaystyle B \cdot \vec{c} \equiv \langle B \vec{c}\rangle_{ 1} $}$$

$$ \langle B \vec{c}\rangle_{ 3} = \langle \vec{c} B\rangle_{ 3}$$ $$\fbox{$ \displaystyle B \wedge \vec{c} \equiv \langle B \vec{c}\rangle_{ 3} $}$$

We can replace $ B$ with

$$ B = \vec{v} I$$
n which $ \vec{v}$ is the dual of $ B$. We of course have

$$ \vec{u} \vec{v} = \vec{u} \cdot \vec{v} + \vec{u} \wedge \vec{v}$$

and multiuplying this by $ I$ gives

$$\begin{eqnarray} \vec{u} \vec{v} I &=& \left( { \vec{u} \cdot \vec{v}} \right) I + \left( { \vec{u} \wedge \vec{v}} \right) I \\ \vec{u} B &=& \left( { \vec{u} \cdot \vec{v}} \right) I + \left( { \vec{u} \wedge \vec{v}} \right) I \\ \vec{u} B &=& \langle \vec{u} B\rangle_{ 3} + \langle \vec{u} B\rangle_{ 1} \\ \vec{u} B &=& \vec{u} \wedge B + \vec{u} \cdot B\end{eqnarray}$$
From that we get

$$ \vec{u} \cdot B = \left( { \vec{u} \wedge \vec{v}} \right) I$$

Let's recap the relation we found between the cross product and the wedeg product.

$$\fbox{$ \displaystyle \vec{a} \times \vec{b} = \left( { \vec{a} \wedge \vec{b}} \right) { I }^{ - 1} $} \qquad \mbox{Cross Product}$$

$$\fbox{$ \displaystyle \vec{a} \wedge \vec{b} = \left( { \vec{a} \times \vec{b}} \right) I $} \qquad \mbox{Wedge Product}$$

We have

$$\begin{eqnarray} I { I }^{ - 1} &=& 1 \\ { I }^{ 2} { I }^{ - 1} &=& I \\ - { I }^{ - 1} &=& I\end{eqnarray}$$
so we can write

$$ \vec{u} \cdot B = - \left( { \vec{u} \wedge \vec{v}} \right) { I }^{ - 1}$$

$$ \vec{u} \cdot B = - \vec{u} \times \vec{v} = \vec{v} \times \vec{u}$$

This means the grade-1 part of $ \vec{u} B$ is the negated cross product of $ \vec{u}$ and the dual of $ B$.

Vector Identities

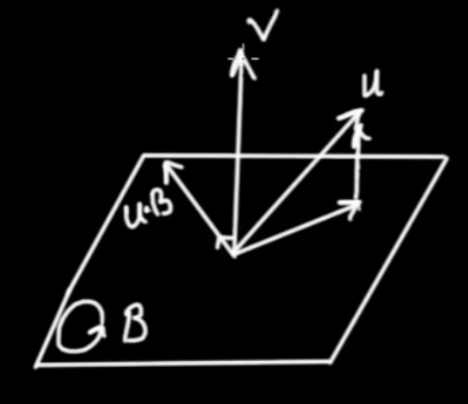$$\fbox{$ \displaystyle \vec{u} \times \left( { \vec{v} \times \vec{w}} \right) = \vec{u} \cdot \left( { \vec{w} \wedge \vec{v}} \right) $}$$

$$\fbox{$ \displaystyle \vec{w} \times \left( { \vec{u} \times \vec{v}} \right) = \left( { \vec{w} \cdot \vec{v}} \right) \vec{u} - \left( { \vec{w} \cdot \vec{u}} \right) \vec{v} $}$$

$$\fbox{$ \displaystyle \vec{a} \cdot \left( { \vec{b} \wedge \vec{c}} \right) = \left( { \vec{a} \cdot \vec{b}} \right) \vec{c} - \left( { \vec{a} \cdot \vec{c}} \right) \vec{b} $}$$

$$\fbox{$ \displaystyle \vec{a} \times \left( { \vec{b} \times \vec{c}} \right) + \vec{b} \times \left( { \vec{c} \times \vec{a}} \right) + \vec{c} \times \left( { \vec{a} \times \vec{b}} \right) = 0 $}$$

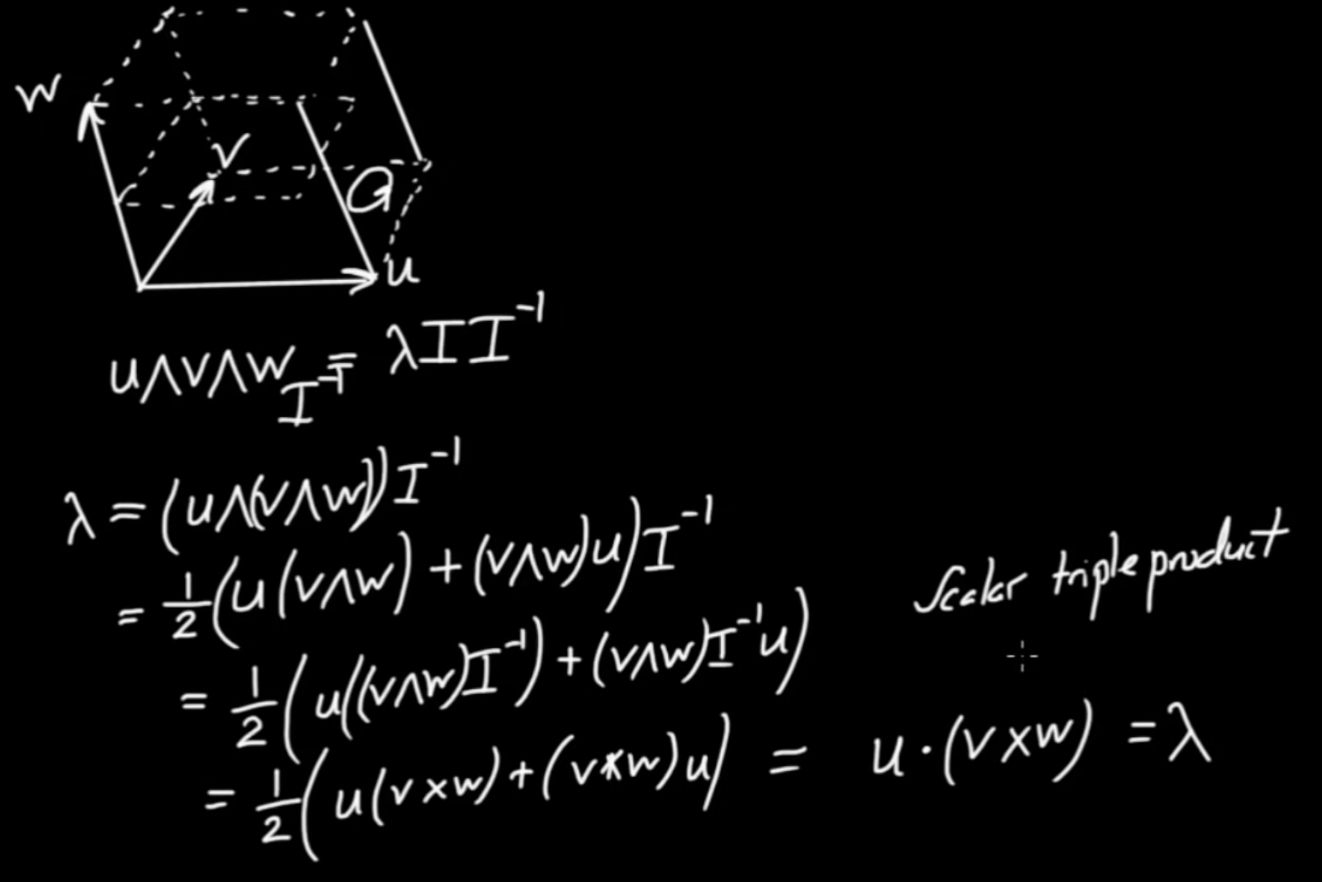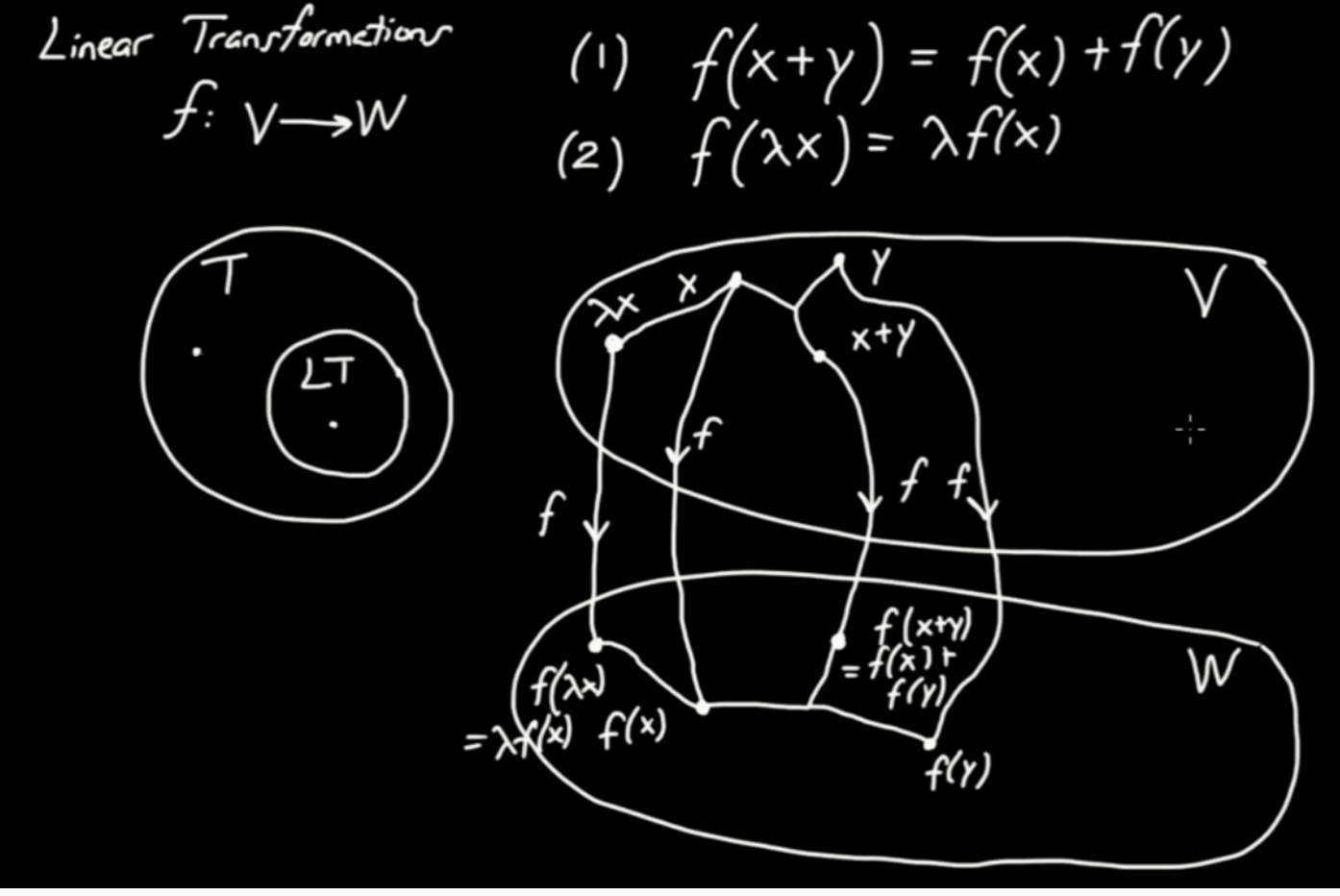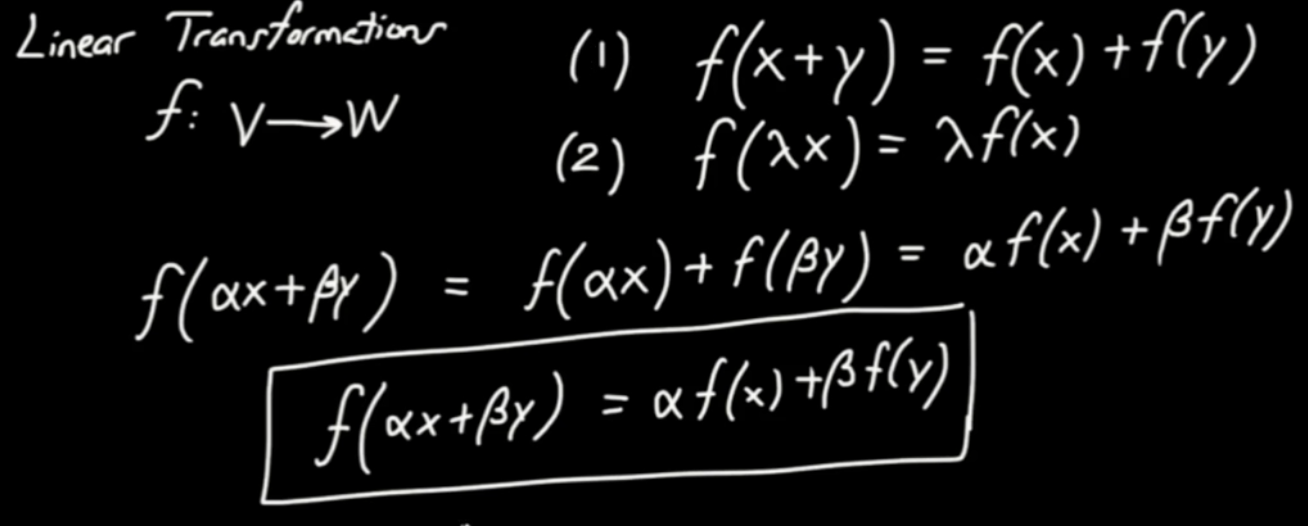Linear Transformations

Matrixes